放射線物理
(74am73,67am69,66.41)
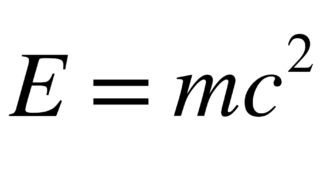
放射線物理学 基礎
粒子としての挙動・運動量P P = M×V ・運動エネルギーT(74am73,62.41) T = 1/2×M×V2 (J=N・m=kg・m2・s-2)・粒子の加速 E(72am70.73、71am76、69am70) E = e×電位差V = 1/2×M×V2 -光速度に近いとき-相対論的力学・運動量P$$P=\frac{M×V}{\sqrt{1-V^{2}/C^{2}}}$$・全エネルギー(70am74) 全エネルギー = T+MC2 = √(P2C2+M2C4) T:運動エネルギー (一般的に放射線のエネルギーEとされるものと等しい) MC2:静止エネルギー$$E={M′C}^{2}-{MC}^{2}={MC}^{2}×(\frac{1}{\sqrt{1-v^{2}/C^{2}}}-1)$$・相対論的質量m′$$P=\frac{M}{\sqrt{1-V^{2}/C^{2}}}$$ M:静止質量・相対論的速度v′$$v′=c×\sqrt{1-{(\frac{{Mc}^{2}}{E+{Mc}^{2}})}^{2}}$$・波長λ:ド・ブロイ波 = h/P ...
問1
波長が0.041nmである光子のエネルギー[keV]はいくつか
ただし、プランク定数=6.6×10-34J・s、光速度=3.0×108m/s、1eV=1.6×10-19Jとする
光子のエネルギーE=Ch/λ[J]より
E[J]=6.6×10-34Js × 3.0×108m/s × 0.041nm
≒482.9×10-17J
E[keV]=482.9×10-17J÷1.6×10-19J/eV
=30keV
使う公式は単純で、定数もすべて与えられているので、簡単な部類の問題
最悪公式を知らずとも単位を合わせていくだけで答えにもたどり着ける
問2
0.025eVの中性子の速度[m/s]はいくつか
ただし、中性子の質量は1.67×10-27kg、1eV=1.60×10-19Jとする
運動エネルギーT = 1/2×M×V2 (J)
0.025eV × 1.60×10-19J = 1/2 × 1.67×10-27 × V2
V≒2.2×103
この問題も使う式自体は単純
ただし、気を付ける必要があるのは基本単位系で、kgをgに直したりすると間違えてしまう
ジュール J:組立単位 kg・m2・s-2, N・mなのでkgはそのまま使う
この辺を変に考えてしまうと間違えてしまうので注意しよう
加速する問題
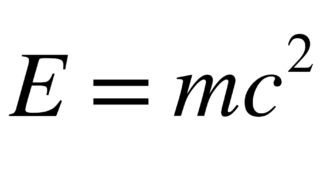
放射線物理学 基礎
粒子としての挙動・運動量P P = M×V ・運動エネルギーT(74am73,62.41) T = 1/2×M×V2 (J=N・m=kg・m2・s-2)・粒子の加速 E(72am70.73、71am76、69am70) E = e×電位差V = 1/2×M×V2 -光速度に近いとき-相対論的力学・運動量P$$P=\frac{M×V}{\sqrt{1-V^{2}/C^{2}}}$$・全エネルギー(70am74) 全エネルギー = T+MC2 = √(P2C2+M2C4) T:運動エネルギー (一般的に放射線のエネルギーEとされるものと等しい) MC2:静止エネルギー$$E={M′C}^{2}-{MC}^{2}={MC}^{2}×(\frac{1}{\sqrt{1-v^{2}/C^{2}}}-1)$$・相対論的質量m′$$P=\frac{M}{\sqrt{1-V^{2}/C^{2}}}$$ M:静止質量・相対論的速度v′$$v′=c×\sqrt{1-{(\frac{{Mc}^{2}}{E+{Mc}^{2}})}^{2}}$$・波長λ:ド・ブロイ波 = h/P ...
問1
光速度の0.8倍に加速された電子の全エネルギーと静止エネルギーとの比、全エネルギー/静止エネルギーはいくつか
式がいくつか登場し、かつ電子の静止エネルギーを把握しておく必要がある
また、これ系の問題は全エネルギー、運動エネルギー、静止エネルギーなのか、または放射線としてのエネルギーなのかをしっかり分けて考えないと間違えてしまうので注意が必要
今回の問題でも、光速度の0.8倍ではなく、1MVで加速した、ならば運動エネルギーはそのまま1MeVになるので計算が非常に楽になる(74am70)
また、電子ではない素粒子を加速する問題も出てくるので対応できるようにしたい
飛程
(74am72, 69am73)
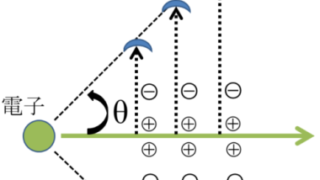
荷電粒子と物質の相互作用
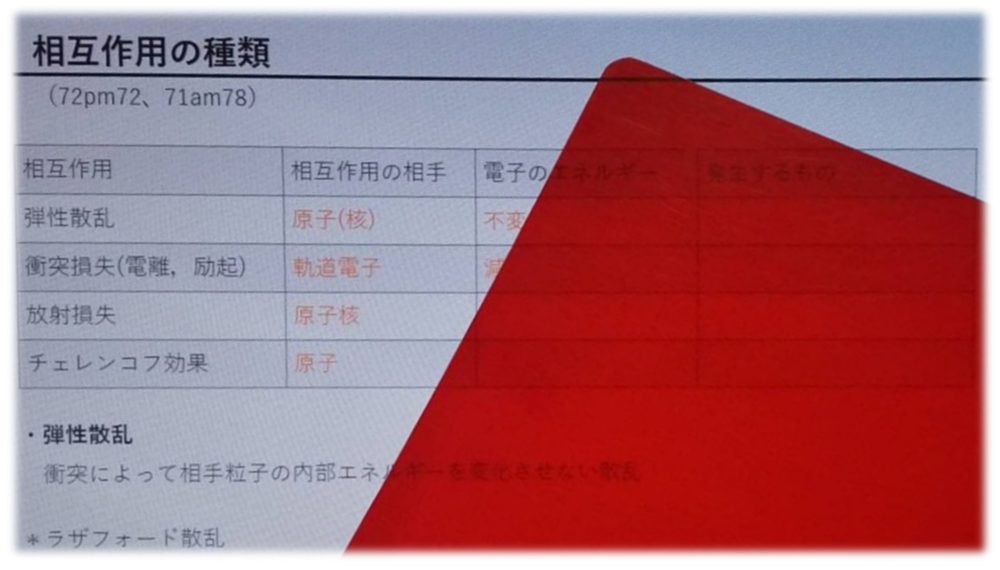
相互作用の種類 (72pm72、71am78)相互作用 相互作用の相手電子のエネルギー発生するもの弾性散乱原子(核)不変なし衝突損失(電離,励起)軌道電子減少 特性X線,オージェ電子放射損失原子核減少制動X線チェレンコフ効果原子減少 青色光・弾性散乱 衝突によって相手粒子の内部エネルギーを変化させない散乱*ラザフォード散乱:ごくまれな確率で原子核と衝突しておこす大角度の散乱・非弾性散乱 衝突によって相手粒子を励起状態にする場合の散乱・制動放射 (63.45) 荷電粒子が原子核の電場により制動を受け、そのエネルギーを光子として放出する現象・電子対消滅 (67am72) 陽電子と電子が対消滅し、その全静止エネルギー(1.022MeV)を180度対向に放出される2つの光子のエネルギー(0.511MeV)として放出する現象・チェレンコフ放射 (68pm73、63.47、60.48) 荷電粒子が透明な誘電物質中(屈折率n)を通過するとき、物質中での光の速度(c/n)を超えた速度(v)で移動した場合に、分極によって位相が重なり、可視光(青色)が放出される現象 屈折率nの大きい物質で発生する 発生時...
問1
12MeVの電子線のアルミニウム中の飛程はいくつか
ただし、アルミニウムの密度は2.7g/cm3とする
エネルギーE[MeV]を12MeVとすると飛程Rは
R≒0.54E-0.13[g・cm-2]
で近似される
R=0.54×12-0.13
=6.35[g・cm-2]
これは面密度当たりの飛程であり、アルミニウムの密度が2.7g/cm3とされているので単位をcmに直すと
R=6.35÷2.7=2.35[cm]
電子線の飛程を計算する問題
電子線の飛程の近似式は下記のようにいくつか存在し、エネルギーや飛程の単位によって変わってくるので注意が必要
国家試験で実際に出題された際はR[cm]=0.5×E/ρで計算したものが正答に一番近い値となっていた
R≒0.5E‐0.3[cm](E=5~50MeV)
≒0.54E-0.13[g・cm-2](0.8MeV<E<3MeV)
問2
10MeVのα線と飛程が等しくなる陽子線のエネルギー[MeV]はいくつか
重荷電粒子の飛程に関する問題は直接飛程の具体的な数値を求める問題より、このような比を求めるような問題が多い傾向
ただし、陽子線の場合は具体的な数字を直接問われる場合も存在するので下記の値を暗記してしまったほうが良いだろう
陽子の飛程:水中で200MeVで約26cm
阻止能
(73pm73,70pm73,68pm73, 66.46.47)

荷電粒子と物質の相互作用
相互作用の種類 (72pm72、71am78)相互作用 相互作用の相手電子のエネルギー発生するもの弾性散乱原子(核)不変なし衝突損失(電離,励起)軌道電子減少 特性X線,オージェ電子放射損失原子核減少制動X線チェレンコフ効果原子減少 青色光・弾性散乱 衝突によって相手粒子の内部エネルギーを変化させない散乱*ラザフォード散乱:ごくまれな確率で原子核と衝突しておこす大角度の散乱・非弾性散乱 衝突によって相手粒子を励起状態にする場合の散乱・制動放射 (63.45) 荷電粒子が原子核の電場により制動を受け、そのエネルギーを光子として放出する現象・電子対消滅 (67am72) 陽電子と電子が対消滅し、その全静止エネルギー(1.022MeV)を180度対向に放出される2つの光子のエネルギー(0.511MeV)として放出する現象・チェレンコフ放射 (68pm73、63.47、60.48) 荷電粒子が透明な誘電物質中(屈折率n)を通過するとき、物質中での光の速度(c/n)を超えた速度(v)で移動した場合に、分極によって位相が重なり、可視光(青色)が放出される現象 屈折率nの大きい物質で発生する 発生時...
問1
8MeVのα線と2MeVの陽子線の質量衝突阻止能の比Sα/Spはいくつか
阻止能の問題
飛程と同様に何かとの比較で出題されることが多い
阻止能は電子線とその他、また放射阻止能と衝突阻止能があり、それぞれ式が異なってくるので混ざらないように注意したい
問2
電子線の鉛における臨界エネルギーはいくつか
Srad/Scol = (E+0.511)×Z÷820
E:電子のエネルギー[MeV]
Z:物質の原子番号
より、鉛は原子番号82なので
1 = (E+0.511)×Z÷820
E ≒ 9.5[MeV]
臨界エネルギーとは同物質においてSrad=Scolとなるエネルギーのこと
実際の国家試験では鉛の原子番号は与えられることが多く、また0.511を抜いた式でも正答を得られるようになっている
光子の相互作用
(73pm72,69am72)

光子と物質の相互作用
光子と物質の相互作用(74pm72、68pm39、68am70、67pm73、64.46、61.47、60.46)相互作用反応相手光子のエネルギー二次電子トムソン散乱自由電子不変なしレイリー散乱軌道電子不変なし光電効果軌道電子消滅 光電子コンプトン散乱自由電子、最外殻電子散乱反跳電子電子対生成原子核消滅 原子、陽電子三電子生成軌道電子消滅 原子、陽電子光核反応原子核 消滅 なし弾性散乱 (69pm71)・光子の波動性を示す反応・トムソン散乱 自由電子との相互作用 光子のエネルギーは変化せず、進行方向が変化する・レイリー散乱(干渉性散乱) 軌道電子との相互作用 光子のエネルギーは変化せず、進行方向が変化する光電効果(75pm72、68am72)・光子のエネルギーEe Ee=Er‐Eb Er:光子のエネルギー Eb:軌道電子のエネルギー・光電子エネルギー K殻光電子<L殻光電子・吸収端 (71pm73、63.46) 光子のエネルギーが各殻の軌道電子放出に必要なエネルギーを上回り、減弱係数が急激に大きくなる場所 エネルギー:L吸収端 < K吸収端 K吸収端のエネルギー:13.6...
問1
0.511MeVのγ線がコンプトン散乱する際の散乱角90度の散乱線エネルギー[MeV]はいくつか
散乱光子のエネルギーを求める問題
散乱光子だけでなく、コンプトン電子やコンプトン端を求める場合もあるので、一通り式は覚えておく必要がある
それぞれ式が多少複雑なので余裕があれば、ということになるか
問2
電子対生成で生じた電子と陽電子の全エネルギーが5MeVのとき、入射光子のエネルギー[MeV]はいくつか
入射光子のエネルギーEr
Er = 2meC2 + Krec +Kp + Ke
Krec:反跳粒子の運動エネルギー
(原子核の場合は≒0)
Kp + Ke:電子対の運動エネルギー
より、Er = 2×0.511 + 5 [MeV]
≒6[MeV]
電子対生成のエネルギー分配に関する問題
コンプトン散乱に比べて非常に簡単で、要は入射光子のエネルギーが電子対の静止エネルギー(2meC2)とその運動エネルギー(Kp + Ke)に分配されるというだけ
基本的に特に言及されない限りKrecは≒0で計算してしまって構わないので、最悪式を知らなくてもエネルギーを保存することを考えれば、電子対の静止エネルギーを失念しない限り、そのまま解けてしまう
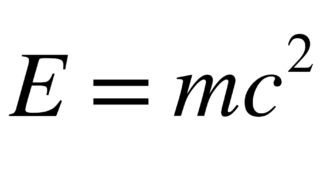
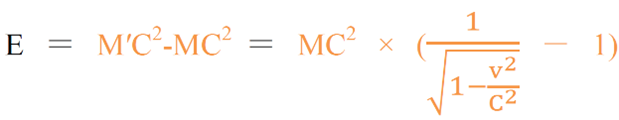



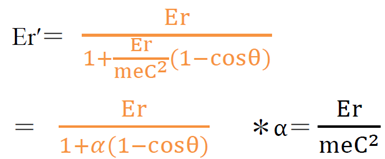






コメント