論理回路とドモルガンの法則
(72am45,71am46,69pm45,68pm45,67am46,66.90)
論理回路 / フーリエ変換
論理回路論理回路とドモルガンの法則 (75pm46、74am45、72am45、71am46、69pm45、68pm45、67am46、66.90、65.90、64.90)・NOT:否定 ・OR:論理和 ・AND:論理積 ・XOR:排他的論理和・NOR:否定論理和 ・NAND:否定論理積 ・ドモルガンの法則 (70pm45、61.57、60.57) 論理和の否定は、否定の論理積に等しい 論理積の否定は、否定の論理和に等しい 2進法、10進法、16進法(75pm47、72pm45、70am45、69am45、68am45、67am45、66.89、65.89、64.89、63.57、61.98)・16進法 → 10進法 10進法で0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15に対応するのが 16進法で0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F つまり10→A、11→B、12→C、13→D、14→E、15→Fとなる 16進法でABCD → 10(A)×163+11(B)×162+12(C)×161+13(D)×160 = 40...
問1
以下に示す語句に対応する論理記号とその論理式を示せ
また、下記の式の右辺を埋めよ
・NOT:否定
・OR:論理和
・AND:論理積
・XOR:排他的論理和
・NOR:否定論理和
・NAND:否定論理積
・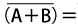
・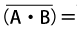
計算問題というよりは暗記の確認問題
論理式に関して、計算は難しくないので、記号と式を間違えずに覚えることが大事
問2
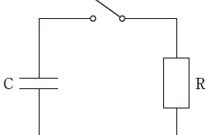
次の論理回路に対応する論理演算式を示せ
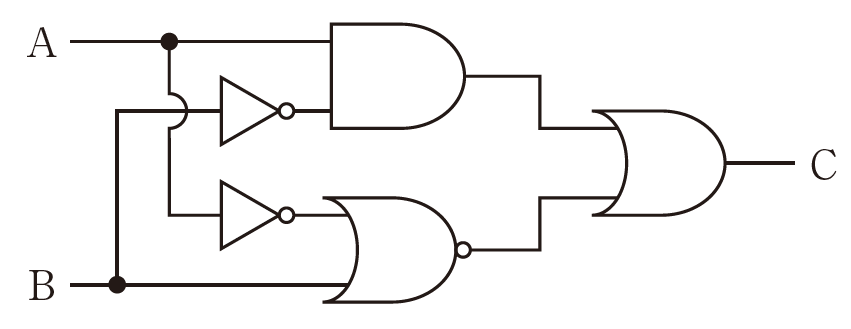
そのまま論理演算式を作っていく問題
否定が入る場合の丸ちょぼだったりを見逃さずに冷静にやれば間違えない
この式にドモルガンの法則を入れ込んだ場合でも解けるようにしておきたい
2進法,10進法,16進法
(73am45,72pm45,70am45,69am45,68am45,67am45,66.89,65.89,64.89,63.57,61.98)
論理回路 / フーリエ変換
論理回路論理回路とドモルガンの法則 (75pm46、74am45、72am45、71am46、69pm45、68pm45、67am46、66.90、65.90、64.90)・NOT:否定 ・OR:論理和 ・AND:論理積 ・XOR:排他的論理和・NOR:否定論理和 ・NAND:否定論理積 ・ドモルガンの法則 (70pm45、61.57、60.57) 論理和の否定は、否定の論理積に等しい 論理積の否定は、否定の論理和に等しい 2進法、10進法、16進法(75pm47、72pm45、70am45、69am45、68am45、67am45、66.89、65.89、64.89、63.57、61.98)・16進法 → 10進法 10進法で0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15に対応するのが 16進法で0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F つまり10→A、11→B、12→C、13→D、14→E、15→Fとなる 16進法でABCD → 10(A)×163+11(B)×162+12(C)×161+13(D)×160 = 40...
問1
2進数1001101110101101を16進数に変換しろ
100110111010110
→1001 1011 1010 1101
=23+22+21+20 23+22+21+20 23+22+21+20 23+22+21+20
=9 11 10 13
=9 B A D
0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15に
対応するのが
16進法で0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
・2進法→16進法
11111111
→1111 1111
=23+22+21+20 23+22+21+20
=15 15
=F F
→FF
この逆パターンもできるようにしておこう
(16進数から2進数への変換)
問2
10進法の12.4を2進法に変換しろ
ただし、小数点は第4位まで表示する
整数部:
12÷2
=6+0 6÷2
=3+0 3÷2
=1+1 1÷2
=0+1
小数点以下:
0.4×2
=0.8 0.8×2
=1.6 0.6×2
=1.2 0.2×2
=0.4 第4位までとあるのでここまで
よって、1100.0110
10進数から2進数への変換かつ、小数点があるバージョン
少し難しいが、ルールさえ覚えていれば解けるし、ルールも難しくはないので覚えておこう
フィルム濃度の計算
(69pm47,68am46,67.93)

フィルム・増感紙・現像 / センシトメトリ / 用語・効果
フィルム・増感紙増感紙-フィルムシステムの構造(両面)フィルム・乳剤 ハロゲン化銀の感度:AgBr>AgCl>AgI AgFは水に溶けやすいので用いられない 高感度乳剤:AgBr+AgI(5%) X線フィルムには蛍光体層がない増感紙 (67am48、62.90)・目的:「蛍光体のX線吸収・発光効率を高く」 「蛍光体の粒子径を大きく」 「支持体の反射率を大きく」 → 感度は向上するが、鮮鋭度は下がる・増感紙の発光スペクトルとフィルムの分光感度 青色発光増感紙 :CaWO4 → レギュラーフィルム 緑色発光増感紙 :Gd2O2S:Tb → オルソフィルム・間接撮影用蛍光板 硫化物蛍光板:(Zn、Cd)S:Ag 希土類蛍光板:Gd2O2S:Tb・保護膜 薄い:鮮鋭度が向上・蛍光体層 蛍光体によって管電圧依存性が変化する(吸収端による) 薄い:感度が低下 鮮鋭度が向上 結合剤を着色:鮮鋭度が向上 クロスオーバ効果:鮮鋭度が低下 現像(現像液)・pH8~13アルカリ性 (64.93、61.90、60.90)・現像主薬:ハイドロキノン(MQ現像液) フェニドン(PQ現像液) ...
問1
透過強度が入射強度の10%となるフィルムAがあり、別のフィルムBを重ねたときに、透過強度が入射強度の5%となった
この時のBの濃度はいくつか
ただし、log102=0.3とする
フィルムAの濃度DAは
DA=log10(100/10)=log1010=1
フィルムAとBを重ねたときに濃度が5%となるので濃度D(A+B)は
D(A+B)=log10(100/5)= log10 (20)= log1010+ log102=1.3
フィルムBの濃度DBは
DB=D(A+B)- DA=0.3
データ量とその送信
(74pm48,71am48,69pm46,67am47)

画像のデジタル化とその保存
標本化(73pm49、65.91、64.94、60pm90) 連続なアナログ信号(連続的信号)をデジタル信号(離散的信号)に変換する処理 標本化が細かいほど解像度は向上するが、元の信号を上回る細かい標本化は意味が無い・サンプリング定理 最適なサンプリング間隔D = 1/(2fmax) fmax:最高空間周波数 ナイキスト周波数 = 1/2d d:サンプリング間隔・エリアシング誤差(75am48、67pm95) ナイキスト周波数よりも高い空間周波数成分が低い空間周波数成分となること このようなアーチファクトはモアレとなって現れる サンプリング間隔がナイキスト周波数に対して広すぎる場合に起こる・アパーチャ効果 ある範囲の平均化による採取によって、捨てる信号を減らし、ノイズ特性が向上するが、平均化によって高周波数成分が減衰し解像度を劣化させること量子化 (65.91、64.94、63.89、60pm90) 標本化したアナログ値(連続値)を整数値(離散値)に変換する処理 Xビット=2X階調 量子化レベル数が大きいほど階調数が多くなるので、濃度分解能が向上し、雑音が減少する実際のDRシステムでは...
問1
マトリクスサイズ2048×2048で1024階調のRAWの画像ファイル容量[MB]を求めよ
ただし、ヘッダ情報は含まない
画像のデータ量[bit]=マトリックスサイズ(M×N)×標本化数×量子化数
記憶媒体にはbyte単位で記憶される
1byte=8bit
また,1Gbyte=1024Mbyte, 1Mbyte=1024Kbyte, 1kbyte=1024byte
より
1024階調=210:10bit
→ 記憶媒体では2byteになる
画像データ[byte]=2048×2048×2
画像データ[Mbyte] =2048×2048×2÷1024÷1024
=8
画像容量の問題で、bitとbyteを間違えないように注意が必要
特に単純な1byte=8bitだけではなく、その処理が1byte毎、つまり9bitも16bitも2byteという単位で処理されることを間違えないように
今回は2次元の画像だが、これが動画や3次元の画像になった場合もう一次元追加されるので計算を間違えないようにしたい
その都度いちいち計算すると単位が膨大になりがちなので、一度すべてを式にまとめてすっきりさせてしまったほうが間違えないだろう
問2
伝送速度1Gbpsのシステムで1枚4Mbyteの画像を送信するとき、1秒間に伝送できる最大の画像枚数はいくつか
伝送速度:1Gbps=1000Mbps
最大画像枚数=1000÷(4×8)=31.25
よって1秒間に完全に送信できる画像の枚数は31枚
伝送速度のbpsはbits per secなので、画像データのほうをbitに変換する
あとはギガとメガの単位さえ間違わなければ大丈夫
画像フィルタ
(72pm47,68pm47,67am49)
デジタル画像処理
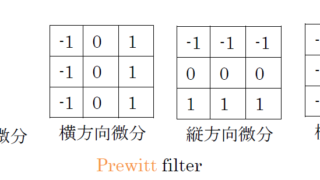
積分処理 複数の画像の画素値の総和を計算する処理 $$g(x,y)=\sum_{k=1}^{n}{f_{k}(x,y)}$$ボケマスク処理(アンシャープマスク処理) (72pm47、69pm48、66.95、63.94、61.94) 高周波成分を強調し、エッジ強調をする g(x,y)=f(x,y)+k fa(x,y):原画像の平滑化画像 k:強調係数ダイナミックレンジ圧縮処理 (67pm45、63.94) 高濃度や低濃度の領域を圧縮、モニタに表示できる濃度範囲を広げる局所的な階調処理 g(x,y)=o(x,y)+f(o_u(x,y)) Ou(x,y):原画像を平滑化した画像 f:処理関数継時的サブトラクション (70am48) 撮影時間の異なる同一被写体の画像間で引き算を行う処理・ワ―ピング処理(非線形処理):位置ずれの補正に使用エネルギーサブトラクション 同一の被写体を異なる管電圧で撮影し、画像間で引き算を行う処理空間フィルタ処理 (75am45、74am45、68pm47、67am49、66.94、61.93、60.96)*Sobelfilterは畳み込み積分し、エッジ...
問1
画像Aに対してフィルタFで処理した時の画素値a(i=3,j=3)を求めよ
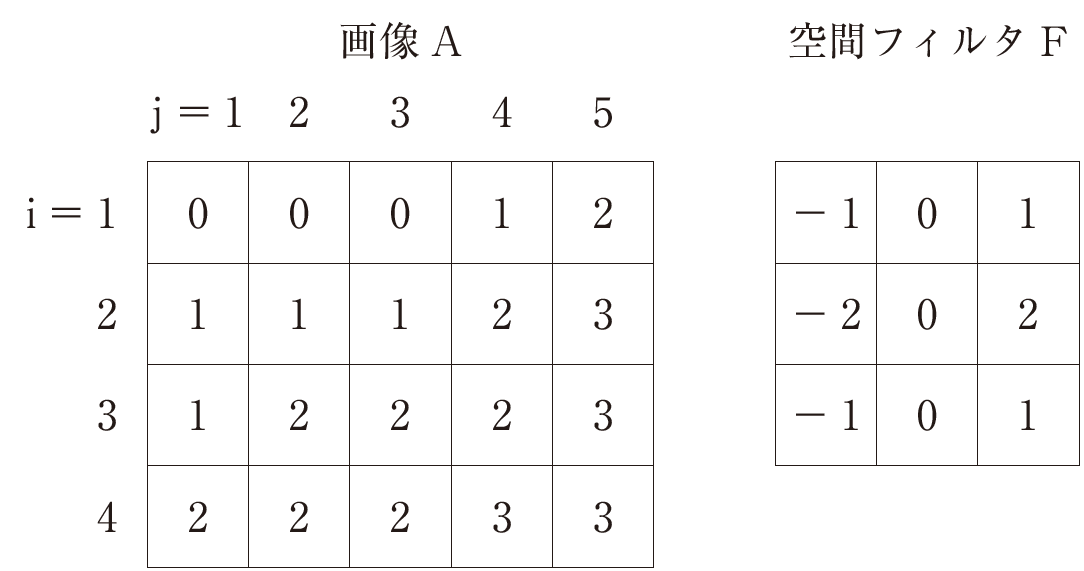
画素値aを中心にしてフィルタのかかる部分を抜き出す
1 2 2
2 2 2
2 2 3
フィルタと重ね合わせる
1×-1 2×0 2×1
2×-2 2×0 2×2
2×-1 2×0 3×1
計算する
-1 0 2
-4 0 4
-2 0 3
すべて足し合わせると2になる
フィルタのかけ方を知っていれば計算は非常に単調なので解ける
この問題の場合はフィルタの値をすべて画像で示しているが、これがある程度文章で出題されても解けるようになっておくと安心できる
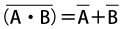
![]()
![]()

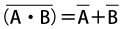





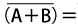






コメント