CT値の計算
(72pm9, 70am11,69pm8)
CT画像 / 3D処理
CT画像 ・CT値 (72pm9、71pm74、70am11、69am10.pm8、67am86、66.78、65.50.pm77.pm83、64am19、64.pm50)$$CT値=\frac{μ_{t}-μ_{w}}{μ_{w}}×1000$$ μt:組織の減弱係数 μw:水の減弱係数臓器・組織CT値臓器・組織CT値骨(皮質)>250灰白質40骨(髄質) 130白質25甲状腺70 脂肪-90肝60血液(凝固)80筋肉・脾・リンパ節45 血液(静脈)55膵40血漿27腎30 浸出液>18・FOV (66.22) CT画像の持つ有効視野で、検出器に依存する 円形の場合は直径、正方形の場合は一辺の長さで表される・ピクセルサイズ CT画像ではマトリックスサイズがほぼ一定なため、FOV/512で計算される・ウィンドウ機能 一般的な階調数は256階調(8bit)(1)ウィンドウ幅(WW):表示するCT値の幅 広い → 小さなCT値差の観察が困難 狭い → 濃淡表示できるCT値の幅が狭い(2)ウィンドウレベル(WL):ウィンドウの中央値 高い → CT画像は黒っぽくなる 低い...
問1
X線の減弱係数が水の1.2倍である組織のCT値[HU]はいくつか
CT値= (μt-μw)/μw ×1000
μt:組織の減弱係数
μw:水の減弱係数
CT値 = (1.2-1)/1 ×1000 = 200
μt:組織の減弱係数
μw:水の減弱係数
CT値 = (1.2-1)/1 ×1000 = 200
一番単純な形の問題
この他にも文章問題でCT値が何を基準としているか、などの問題も出題されている
また、今回はストレートにCTが穴埋めになっているが、このままではなく減弱係数を穴埋めにする場合もある
この他にも文章問題でCT値が何を基準としているか、などの問題も出題されている
また、今回はストレートにCTが穴埋めになっているが、このままではなく減弱係数を穴埋めにする場合もある
問2
CT値が85HUである組織の減弱係数μaと、CT値が10HUである組織の減弱係数μbの比μa/μbはいくつか
CT値= (μt-μw)/μw ×1000
より
μt=μw(1+CT値/1000)
比をとると
μa/μb=(1+85/1000)/(1-10/1000)≒1.07
より
μt=μw(1+CT値/1000)
比をとると
μa/μb=(1+85/1000)/(1-10/1000)≒1.07
CT値の式を変形させて、かつ比をとる問題
覚えることは増えないが、式の変形に時間を取られると少しやっかいになってしまう
実際に出題された問題では、選択肢5つのスケールがだいぶ違うので大雑把な計算で選択肢は絞れるので、ざっくり計算で終わらせてしまうのも良いか(1.01、1.1、2をざっくり代入する)
覚えることは増えないが、式の変形に時間を取られると少しやっかいになってしまう
実際に出題された問題では、選択肢5つのスケールがだいぶ違うので大雑把な計算で選択肢は絞れるので、ざっくり計算で終わらせてしまうのも良いか(1.01、1.1、2をざっくり代入する)
ピッチファクタ
(71pm7,69am9)

CT画像 / 3D処理
CT画像 ・CT値 (72pm9、71pm74、70am11、69am10.pm8、67am86、66.78、65.50.pm77.pm83、64am19、64.pm50)$$CT値=\frac{μ_{t}-μ_{w}}{μ_{w}}×1000$$ μt:組織の減弱係数 μw:水の減弱係数臓器・組織CT値臓器・組織CT値骨(皮質)>250灰白質40骨(髄質) 130白質25甲状腺70 脂肪-90肝60血液(凝固)80筋肉・脾・リンパ節45 血液(静脈)55膵40血漿27腎30 浸出液>18・FOV (66.22) CT画像の持つ有効視野で、検出器に依存する 円形の場合は直径、正方形の場合は一辺の長さで表される・ピクセルサイズ CT画像ではマトリックスサイズがほぼ一定なため、FOV/512で計算される・ウィンドウ機能 一般的な階調数は256階調(8bit)(1)ウィンドウ幅(WW):表示するCT値の幅 広い → 小さなCT値差の観察が困難 狭い → 濃淡表示できるCT値の幅が狭い(2)ウィンドウレベル(WL):ウィンドウの中央値 高い → CT画像は黒っぽくなる 低い...
問1
1回転0.5秒の64列マルチスライスCT装置を用いて、コリメーション幅0.625mm、テーブル移動速度8cm/sで撮影したときのビームピッチはいくつか
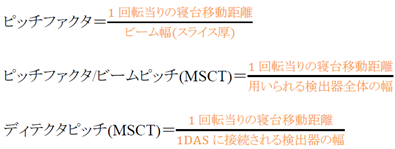
ビームピッチ=80mm/s×0.5s÷(0.625mm×64)=1.0
基本的なピッチファクタに関する計算問題
この場合は出ている数字すべて使うだけで良いので簡単
ピッチファクタが穴埋めでなくて、他の因子が穴埋めであっても式の変形もそこまで難しくならないので冷静に対処すれば大丈夫
この場合は出ている数字すべて使うだけで良いので簡単
ピッチファクタが穴埋めでなくて、他の因子が穴埋めであっても式の変形もそこまで難しくならないので冷静に対処すれば大丈夫






コメント