コンデンサ式高電圧装置
(73pm11,64.54)
問1
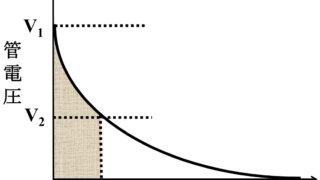
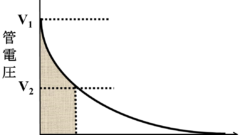
容量0.5μFのコンデンサ式X線装置において、充電電圧80kVで10mAs放出した時の波尾切断電圧[kV]はいくつか
C:静電容量[μF]
Vc:充電電圧[kV]
Vd:波尾切断電圧[kV]
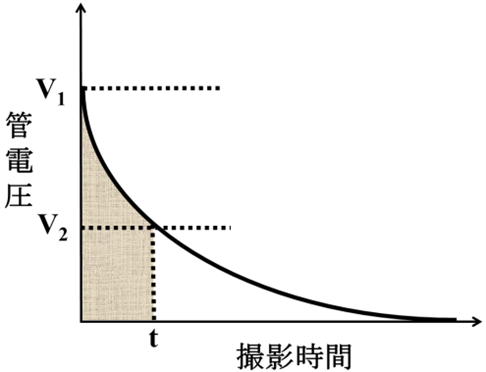
Vd=Vc‐mAs/C
=80‐10/0.5 =60
基本的には左辺に放電電荷量をとると右辺の変数が3つになり、どこが問われるのかはわからないが、過去問的には波尾切断電圧が問われているので式を変形しなければならない
式の形だけではなく、[ ]の中の単位も覚えてないと間違えうるので注意が必要
X線管入力の動作特性
(72am12,71am9,67pm6)
問1
三相12ピーク整流装置で、撮影管電圧100kV、管電流1000mAのときの電力[kW]はいくつか
P = U×I×f×10-3
U:管電圧[kV],ピーク値で表される
I:管電流[mA],平均値で表される
f:管電圧のリプル百分率によって定まる定数
f=1.0:リプル百分率が10%以下の場合
(インバータ式, 定電圧形, 三相12 ピーク形に相当)
f=0.95:リプル百分率が10%を超え25%以下の場合
(三相6ピーク形に相当)
f=0.74:リプル百分率が25%を超える場合
(単相2 ピーク形, 単相1ピーク形に相当)
P =100×1000×1.0×10-3
=100
問題としては、リプル百分率で決める場合と整流方式(三相6ピークなのか12ピークなのかなど)で決める場合がある
管電圧の単位はkV(ピーク値)、管電圧の単位はmA(平均値)なのでこれも注意が必要
問2
短時間負荷が100kV、320mAのとき、X線管入力が30.4kWである場合、管電圧のリプル百分率[%]はいくつか
P = U×I×f×10-3
U:管電圧[kV],ピーク値で表される
I:管電流[mA],平均値で表される
f:管電圧のリプル百分率によって定まる定数
f=1.0:リプル百分率が10%以下の場合
(インバータ式, 定電圧形, 三相12 ピーク形に相当)
f=0.95:リプル百分率が10%を超え25%以下の場合
(三相6ピーク形に相当)
f=0.74:リプル百分率が25%を超える場合
(単相2 ピーク形, 単相1ピーク形に相当)
30.4=100×320×f×10-3
f=0.95
よってリプル率は10%を超え25%以下となる
実際に出された問題では、選択肢が5つある中で当てはまるものが一つだけになっていた
整流方式が書かれてあっても解けるようにしておきたい
短時間負荷
(70am5)
問1
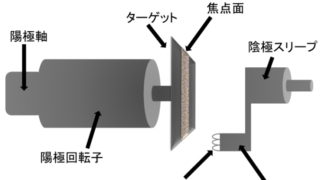
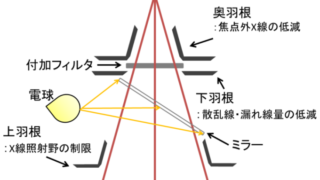
回転陽極X線管で焦点軌道半径を20%大きくした場合の0.1s以下の短時間許容負荷の変化量はいくつ
W∝√(D×N)
D:焦点軌道直径
N:陽極回転速度
W∝√1.2≒1.1
よって短時間許容負荷Wは1.1倍に増える
θ:ターゲット角度(l/sinθは実焦点の長さ)
l:実効焦点の長さ
b:実効焦点の幅(実焦点の幅と同じ)
D:焦点軌道直径
N:陽極回転速度(電源周波数に比例し、普通回転形:約3000回転/分、三倍高速回転形:約9700回転/分)
高電圧変圧器
(70pm5)

問1
巻線比n2n/1=500の単相2ピーク形X線高電圧装置で、管電流500mAを流した時の一次電流[A]はいくつか
n1:コイルの一次側巻数
n2:コイルの二次側巻数
V1:一次側の電圧(実効値で表示)
V2:二次側の管電圧(最大値で表示)
I1:一次側の電流(実効値で表示)
I2:二次側の管電流(平均値で表示)
かつ
では単相2ピーク形、実効値=最大値×1/√2 、実効値=平均値×π/2√2
500=I1/0.5
V1=250mA(平均値)
V1(実効値)=250×π/2√2≒278
一応式の全貌を下記に示すが、よっぽど余裕がない限り、これをすべて覚えるなら他にリソースを回したほうがコスパは良い
管電圧はピーク値,管電流は平均値を示すため換算して扱う
n2/n1 = a = V2/V1 =I1/I2
n1:コイルの一次側巻数
n2:コイルの二次側巻数
a:巻数比
V1:一次側の電圧(実効値で表示)
V2:二次側の管電圧(最大値で表示)
I1:一次側の電流(実効値で表示)
I2:二次側の管電流(平均値で表示)
・ピーク時,実効値,平均値の関係
→管電圧波形(X線高電圧装置による)で変わる
(1)インバータ式,定電圧形,三相12ピーク型
実効値≒ピーク値
かつ 実効値≒平均値
(2)三相6ピーク形
実効値=最大値×0.956
かつ 実効値≒平均値
かつ 最大値=平均値×π/3
(3)単相2ピーク形
実効値=最大値×1/√2
かつ 実効値=平均値×π/2√2
(4)単相1ピーク形
実効値=最大値×1/2
かつ 実効値=平均値×π/2






コメント