抵抗・コンデンサ・コイル / 直流回路 / 並列回路

抵抗・コンデンサ・コイル

抵抗R

　（72am75、65.56、64.52、63.53、62.55）

　単位：Ω(オーム)＝1/S(ジーメンス)
　電流の流れにくさを表す
　電流の流れやすさはコンダクタンスという
　抵抗R＝ρ×長さl［m］÷断面積S［m²］
　　　　ρ：抵抗率（比抵抗）［Ω・m］

*倍率器(73pm77)

コンデンサ

・静電誘導　
　導体外部からの電界により電荷が導体表面に移動する現象

・静電容量
（76am75、74pm77、71am75、70pm75、69pm75、68pm76、67am74、61.51）
　単位：F（ファラド）
　二つの導体（コンデンサ）に電圧Vを印加すると+q、-qの電界が誘起される
　静電容量C　＝　q / V［F＝A・s/V＝C/V］
　蓄積されるエネルギーW　＝　CV²×1/2

・平行平板コンデンサの静電容量C［F］
　（76pm77、72am77）
　C［F］＝ε×S［m²］÷d［m］
　ε：誘電率

・交流回路では電圧Vの位相は、電流Iに対して90°遅れる
　Vc　＝　1/wc　×　I₀　×　sin(wt-π/2)

コイルL

・電磁誘導
　コイル内の磁束の変化によって起電力が誘導される現象

・レンツの法則　（68am75）
　電磁誘導で流れる電流は磁力線に対して抵抗する向きに流れるという法則
　
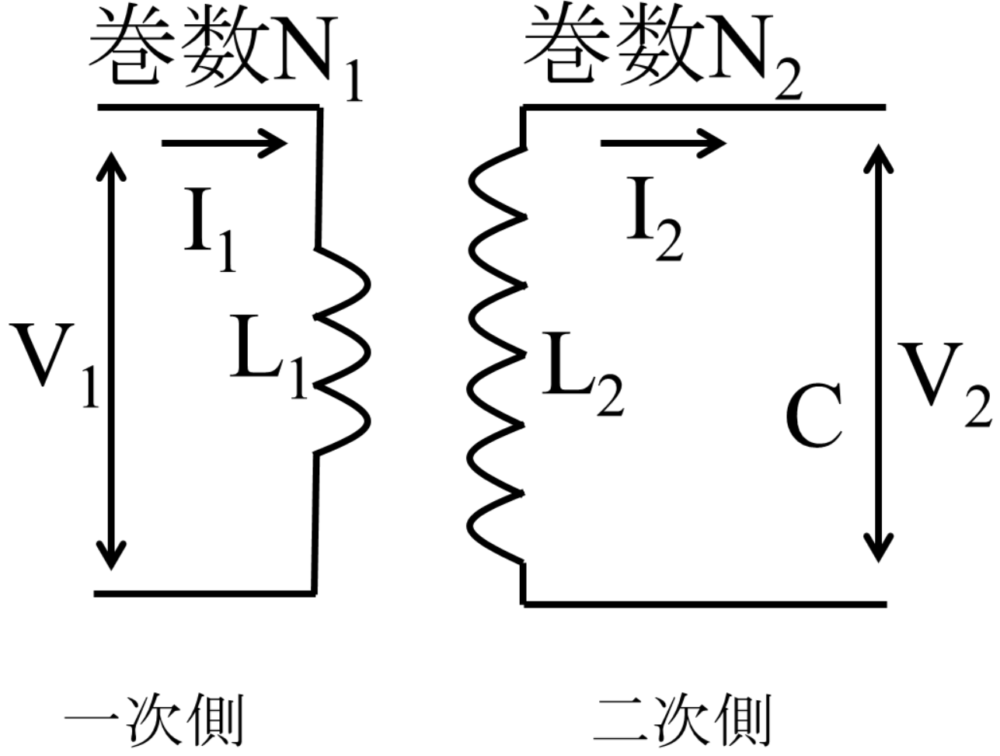
・ファラデーの電磁誘導側　
（69am75、68am75）
　コイルの巻き数がN回のとき、誘導起電力はN倍になる

・自己インダクタンスL　
（75pm75、67pm76、66.51、61.51）
　単位：H＝wb/A

　コイルに電流Iを流すと鎖交磁束N・Φ［wb］が発生する
　自己インダクタンスL　＝　N×Φ÷I　［H］
　N：巻き数　Φ：磁束

　コイルに蓄積されるエネルギーW　（66.51）
　W　＝　L×I²×1/2

・誘導起電力V（70pm76）
　V＝-n×dΦ/dt

・交流回路では電圧Vの位相は電流Iに対して90°進む
　VL　＝　wL　×　I₀　×　sin(wt+π/2)

＊ソレノイド：3次元のコイル　(69am75)

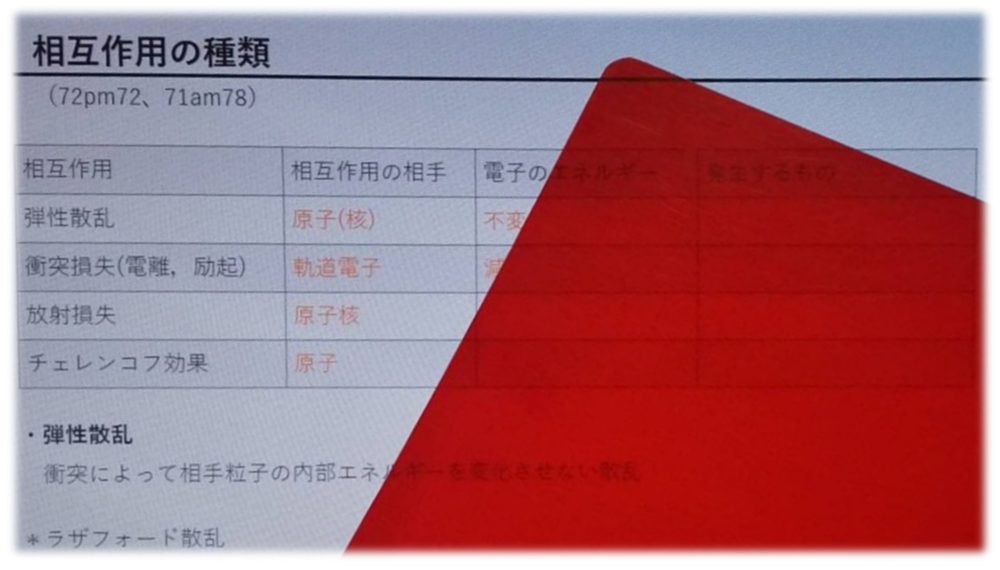
＊コッククロフトオォルトン加速器　(71am77)

直流回路

オームの法則

　（75am77、72pm78、65.52、61.53、60.53）

　電流I＝電圧V÷抵抗R

・消費電力W＝V²÷R　
　　　　　　＝R×A²

抵抗の直列接続

・合成抵抗R＝R1+R2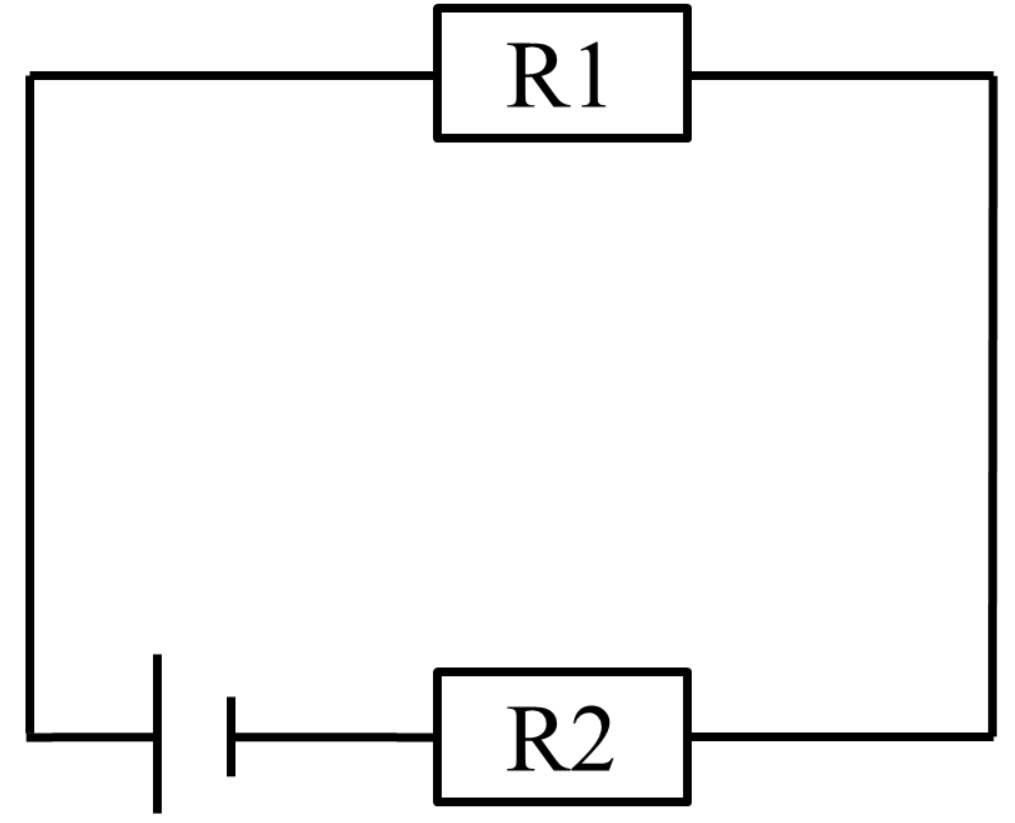

抵抗の並列接続

(74pm76、72pm75、69pm77、65.52)
　合成抵抗R＝R1R2/(R1+R2)
　または、R＝1/R1+1/R2+1/R3+…+1/Rn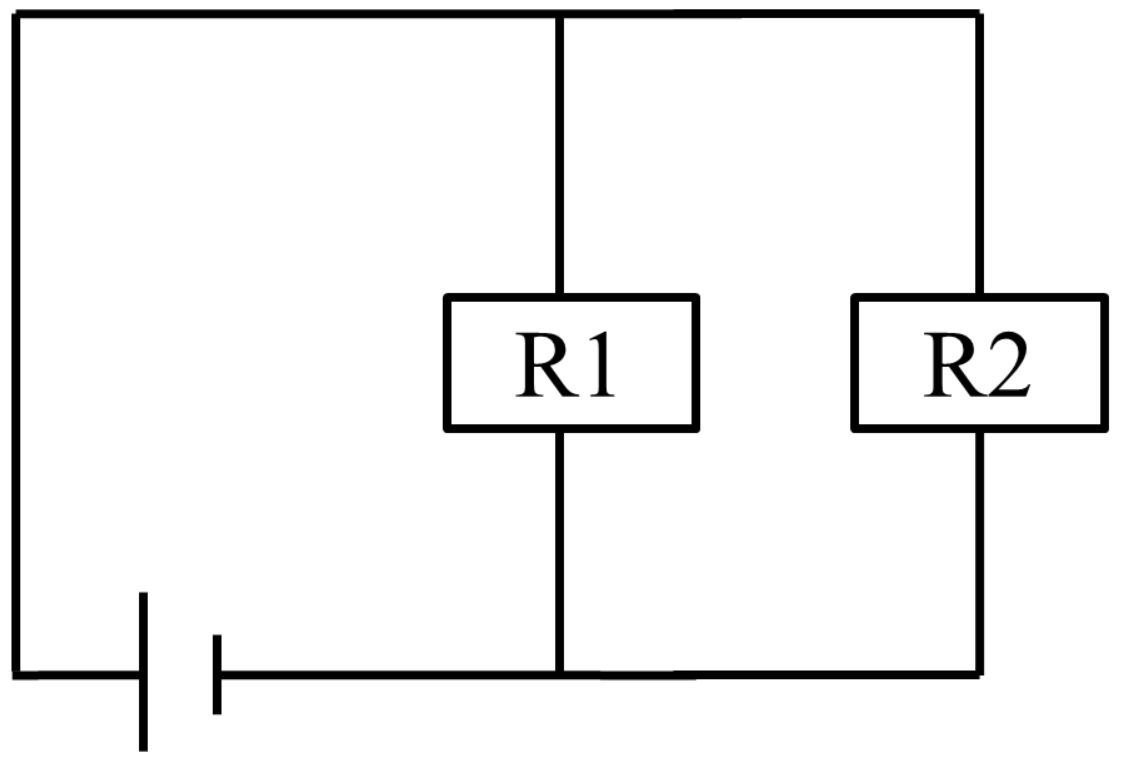

ブリッジ回路

　(76pm76、69pm76)

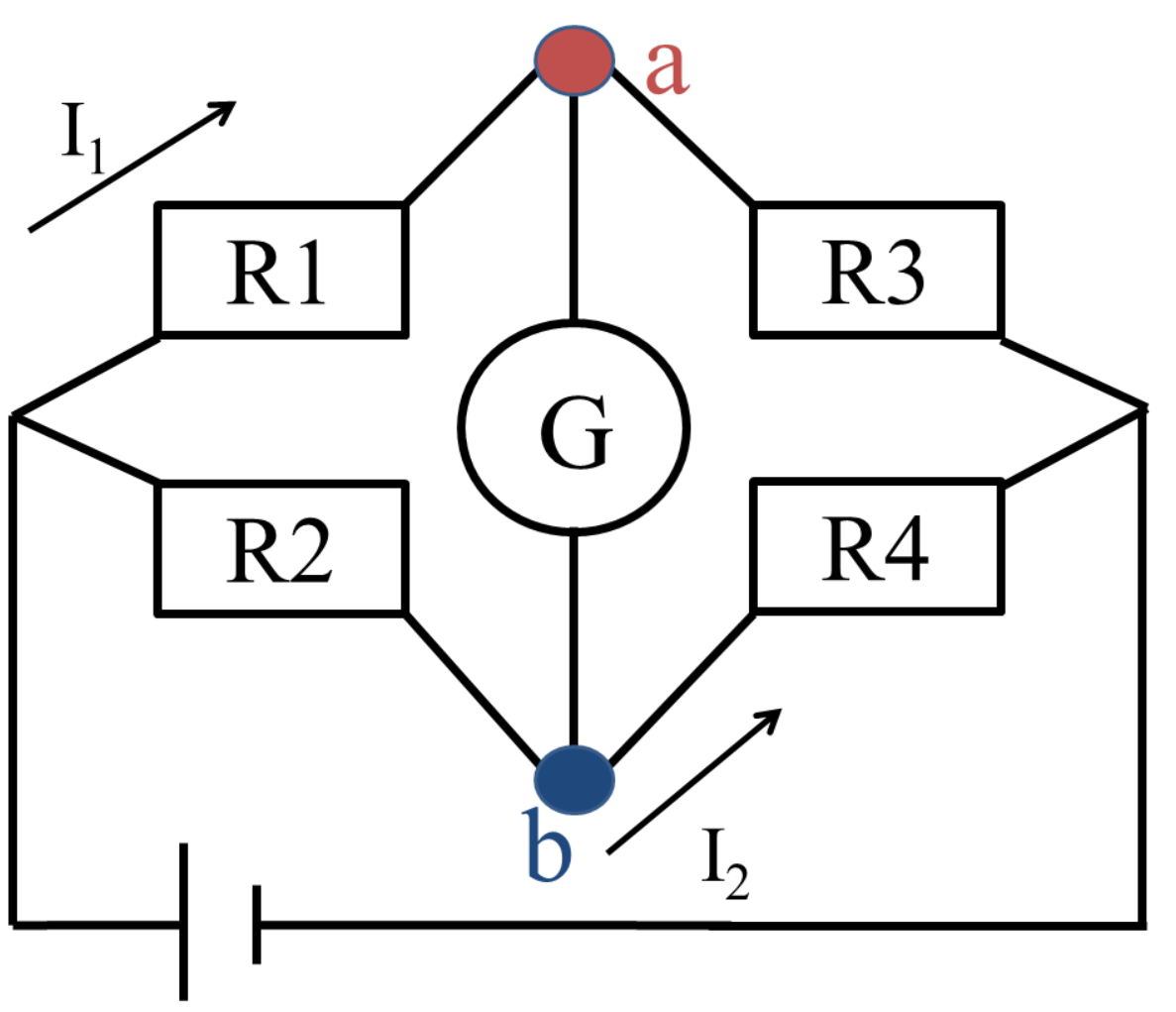
　Gの電流が0のとき、a、bの電圧は同じで差がない
　I1＝V÷(R1+R3)
　I2＝V÷(R2+R4)
　Va＝I1×R3
　Vb＝I2×R4
　よって
　R1×R4＝R2×R3
　また
　R1/R2＝R3/R4　(平衡条件)

コンデンサの直列接続

(74am76、69pm75、66.52、62.53)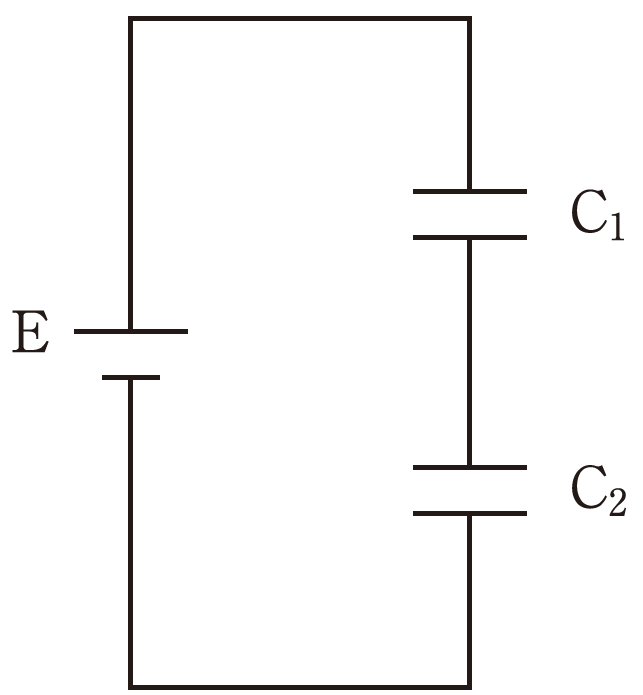

　V1：V2＝1/C1：1/C2
　1/C＝1/C1+1/C2
　合成容量C＝C1C2/(C1+C2)
　また、
　C1の電荷Q1＝C2の電荷Q2
　E＝V1+V2
　V1=Q1÷C1
　V2=Q2÷C2

医用工学　計算ドリル

抵抗、コンデンサ、コイル （73pm77,72am75.77pm75,70am76,66.54） 問1 　1種類のキャリアのみを有する半導体の導電率が102S・m-1、移動速度が0.36m2・V-1・s-1であるとき、キャリア濃度［m-3］はいくつか 　ただし、キャリアの電荷を1.6×10-19Cとする 答えキャリア濃度＝102÷（0.36×1.6×10-19） 　　　　　　　　＝1.7×1021［m-3］ 解説　抵抗ではなく半導体だが、例としてよかったので掲載 　問題だけだと何を言っているのかわからない学生が多く、難問になりそうだが、実はそうでもない、という問題 　今回の問題のように、各数字と答えの単位が書いてあり、他に定数を覚えている必要がない場合、出てきている数字の単位（今回であれば3つ）を組み合わせて、答えの単位に合わせるだけで良いので公式等を知らなくても簡単に解けてしまう 　今回の場合はSがオームの逆数なのを知っていれば 　導電率：S・m-1→Ω-1・m-1→A・V-1・m-1 　移動速度：m2・V-1・s-1 　電荷：C→A・s 　なので、導電率を移動速度と電荷で割ればよい...

radiological.site

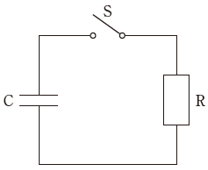
交流回路

直列接続

　（75pm77、72am76、64.53、62.56）

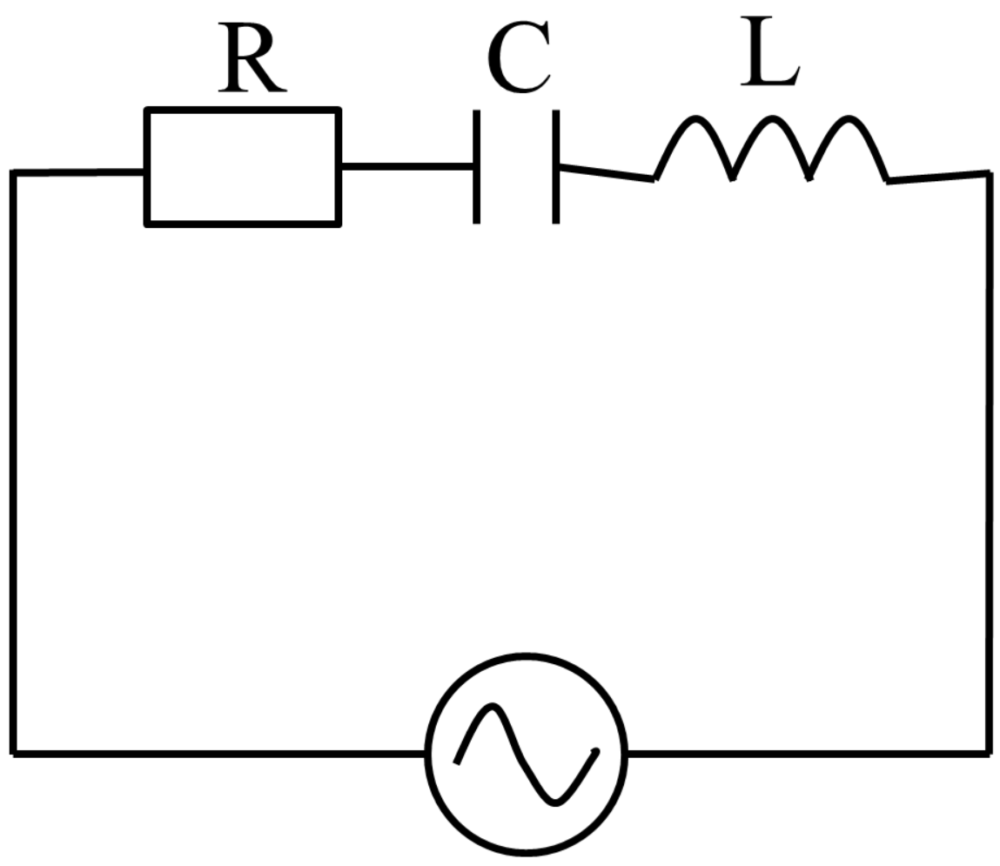
・抵抗R　
：V＝I×R　
　V/I＝R［Ω］

・コンデンサC　
：V＝I/(ωC)　
　V/I＝1/ωC［Ω］

・コイルL　
：V=ωL×I
　V/I＝ωL［Ω］

・合成インピーダンスZ
　Z　＝　R　+　ωL　+　1/ωC
　　　＝　R　+　（ωL－1/ωC）

・Zの大きさ
$$｜Z｜＝\sqrt { R^{ 2 }+(ωL-\frac { 1 }{ ωC } )^{ 2 } } $$
　ωL-1/ωC：リアクタンス

＊角周波数ω　＝2πf

・直列共振(電圧共振)　

（71pm75、67am76）
　ωL＝1/ωCの時、以下の条件になる
「Lにかかる電圧VL＝Cにかかる電圧LC」
「Z=R」
「電流Iは最大」
「電流と電圧の位相が等しくなる」
　共振角周波数ω0＝1/√LC
　共振周波数f0＝1/2π√LC　(70pm76、65.54)
　＊角周波数ω＝2πf

・コイルの良さを示すQ

　Q　＝　ω0L÷R
　　　=　1/ω0CR　
　　　＝　1/R　×√L/C
　直列共振のとき、大きな電圧を取り出せるので、電圧共振とも呼ぶ
　ω0＝2πf0

・振動数ν

　ν＝Asin(Bt+x)
　A：電圧または電流　
　B：角周波数ω［rad/s］　
　X：位相差

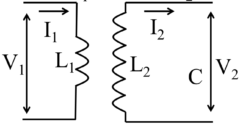
並列接続

・アドミタンスY
　Y　＝　1/R　+　 jωC　+　1/jωL
　　　＝　R　+　j（ωC－1/ωL）

・Yの大きさ

$$｜Y｜＝\sqrt { R^{ 2 }+(ωC-\frac { 1 }{ ωL } )^{ 2 } } $$

・並列共振　（67am76）
　ωC＝1/ωLの時、以下の条件になる
「Lを流れる電流IL＝Cを流れる電流IC」
「Rを流れる電流は電源電流と等しい」

医用工学　計算ドリル

抵抗、コンデンサ、コイル （73pm77,72am75.77pm75,70am76,66.54） 問1 　1種類のキャリアのみを有する半導体の導電率が102S・m-1、移動速度が0.36m2・V-1・s-1であるとき、キャリア濃度［m-3］はいくつか 　ただし、キャリアの電荷を1.6×10-19Cとする 答えキャリア濃度＝102÷（0.36×1.6×10-19） 　　　　　　　　＝1.7×1021［m-3］ 解説　抵抗ではなく半導体だが、例としてよかったので掲載 　問題だけだと何を言っているのかわからない学生が多く、難問になりそうだが、実はそうでもない、という問題 　今回の問題のように、各数字と答えの単位が書いてあり、他に定数を覚えている必要がない場合、出てきている数字の単位（今回であれば3つ）を組み合わせて、答えの単位に合わせるだけで良いので公式等を知らなくても簡単に解けてしまう 　今回の場合はSがオームの逆数なのを知っていれば 　導電率：S・m-1→Ω-1・m-1→A・V-1・m-1 　移動速度：m2・V-1・s-1 　電荷：C→A・s 　なので、導電率を移動速度と電荷で割ればよい...

radiological.site