ROC曲線解析
(76pm95、75pm95、74pm95、73am95、68am95、67pm96、65.90、63.91.92、60.92)
主観的な総合画像評価法
・ROC曲線を求める方法
(1)評定手続き
・評定確信度法
:5段階のカテゴリーは良く用いられる
・連続確信度法
:カテゴリーを設けず、連続スケールで評価する
(2)二段階評価手続き
Yes or Noの二通りの評価を行う
・読影者間の能力差を評価できる
・異なるモダリティ間の解析にも使用可能
・評定の難易度に影響される
ROC曲線
(70am65)
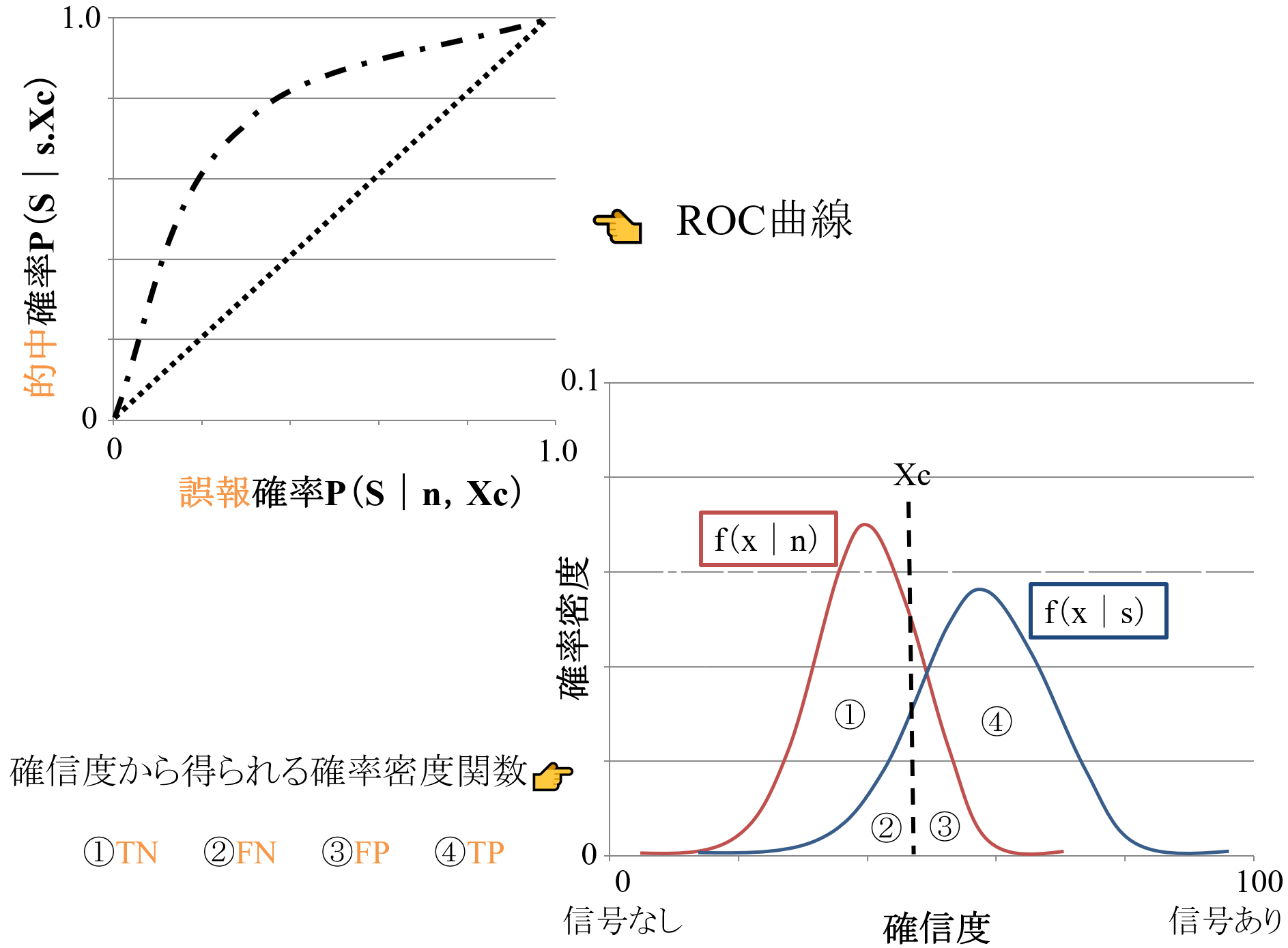
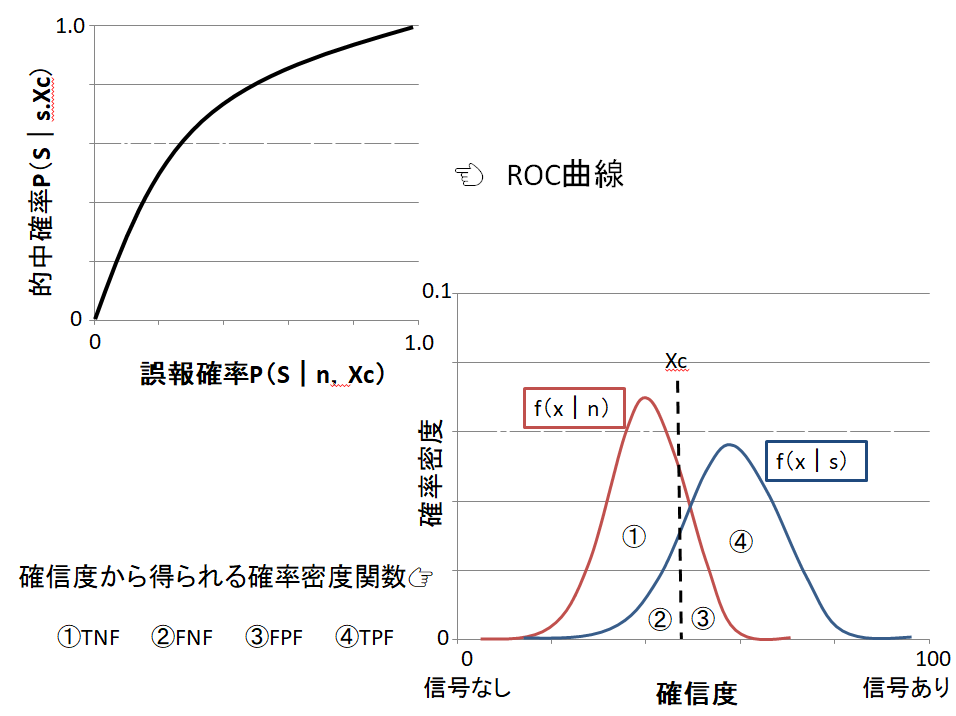
・縦軸:真陽性率(的中確率)
・横軸:偽陽性率(誤報確率)
・ROC曲線下面積Az
Az:0.5≦Az≦1.0
Azは大きいほど評価が良い
2択法では正答率と同等になる
・刺激-反応行列
| 反応あり | 反応なし | |
| 刺激あり | TP | FN |
| 刺激なし | FP | TN |
・評価の要素
(72pm94、71pm46.94、69pm95、68pm95、65.91、64.92、63am27、62.88、61am22.pm92)
※(1)+(4)=1 (2)+(3)=1
以下、判定点xにおけるそれぞれの確率
(1)真陽性率(TPF、感度、ヒット)
$$P(S|s)=∫_{ a }^{ ∞ }(X|s)dx$$
(2)偽陽性率(FPF、虚報)
$$P(S|n)=∫_{ a }^{ ∞ }(X|n)dx$$
(3)真陰性率(TNF、特異度、無病正診率)
$$P(N|n)=∫_{ -∞ }^{ a }(X|n)dx$$
(4)偽陰性率(FNF、ミス)
$$P(N|s)=∫_{ -∞ }^{ a }(X|s)dx$$
・評定の難易度に影響される
*陽性的中率(PPV)(76am94、70am94)
$$PPV=\frac { (TPF×a) }{ (TPF×a)+(1-TNF)×(1-a) } $$
a:有病率
・ROC曲線間の統計的有意差検定
(77pm95、72pm95、66.91、63.91、62.90)
t検定
:観察者間変動を考慮
Jackknife
:観察者間変動と資料間変動を考慮
・その他ROCの解析
(1)FROC曲線(自由応答ROC解析)
複数の信号に対する評価(数はいくつでも選択可能)
縦軸:真陽性率
横軸:一画像当たりの偽陽性数
(2)LROC曲線(位置決定ROC解析)
(65.91)
信号の有無だけでなく位置も認知させる解析法
平均ROC曲線
(1)アベレージ法
:観察者間の変動が大きい場合それぞれが観察者のFPFにおける全観察者のTPFの平均値を求める方法
(2)プール法
:試料ごとに観察者の評定値を平均化して求める方法
画像試料ごとに平均化した値を求める。
プール法で得られたROC曲線は真のROC曲線よりも悪くなる傾向を示すので、アベレージ法が推奨される
DQE(検出量子効率)
(77pm93、76am95、71pm95、70pm48、69am95、68am93、66.92、65.92、62.89.92)
物理特性的総合画像評価でX線光子の利用率を示す
$$DQE=\frac { loge^{ 2 }×G^{ 2 }×MTF^{ 2 } }{ WS×q } $$
= (出力画像のSN比)2/(入力画像のSN比)2
= NEQ/q
NEQ:雑音等価量子数
G:デジタル特性曲線のグラディエント
q:単位面積当たりの量子数
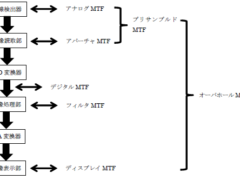
MTF:プリサンプルドMTF
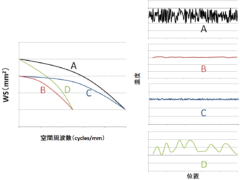
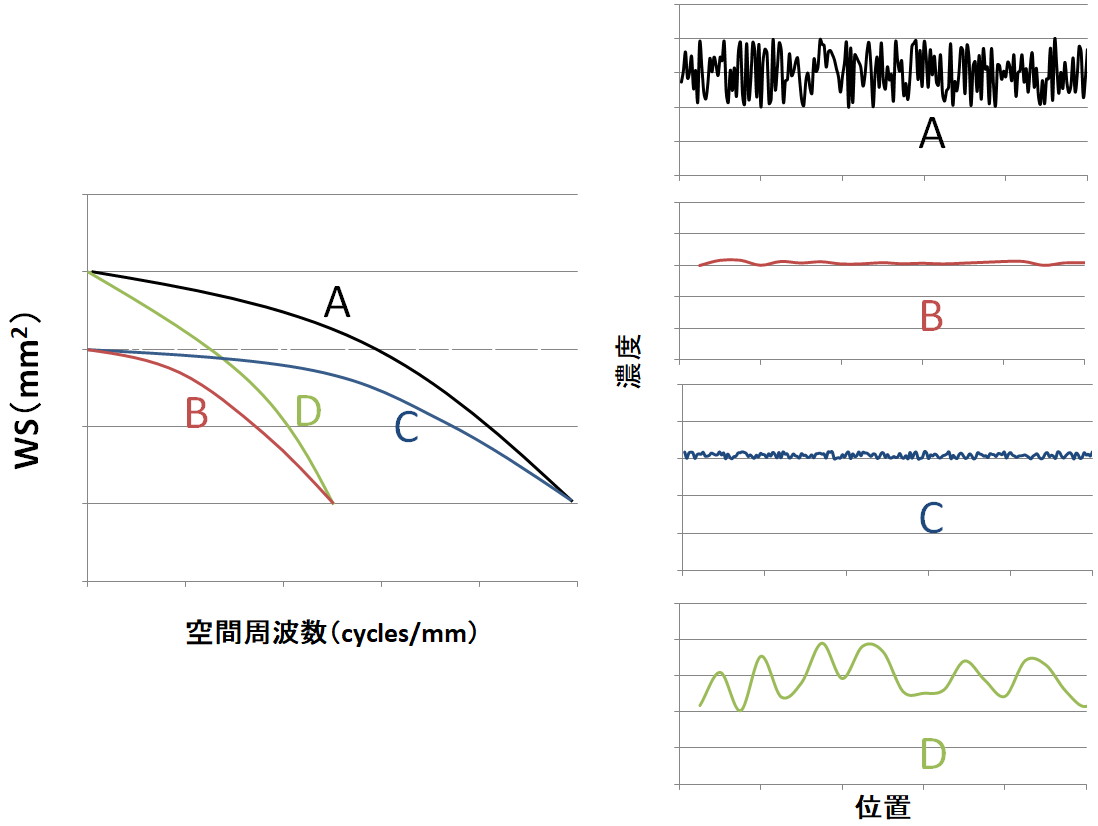
WS:デジタルウィナースペクトル
・横軸:空間周波数
・DQEが理想的な検出器はDQE=1
(最大値は1)
・高周波数でDQEは低下する
・DQEが同じ画像でもMTFとWSは違う可能性がある






コメント
刺激反応マトリックスについて、
TPF等は割合なのでTPFはTPにするべきだと思います。他も同様です。
ご指摘ありがとうございます
訂正させて頂きました