医用工学 トップページ

電荷・電界・電位差(電圧) 電荷(量)Q 　単位：C(クーロン) 　電荷素量e 　e　＝　1.602×10-19［C］　 2個の静電荷に働くクーロン力　（63.51）　クーロン力F　　　$$F＝\frac { 1 }{ 4πε_{ 0 } } ×\frac { g_{ 1 }×g_{ 2 } }{ r^{ 2 } } ＝9×{ 10 }^{ 9 }×\frac { g_{ 1 }×g_{ 2 } }{ r^{ 2 } }$$ 　r：距離　g：電荷　ε0：真空の誘電率電界(1つの電荷が力を及ぼす空間) 　電界の強さE　　 E　＝　「電気力線の数」÷「表面線［m2］」・点電荷から距離r［m］での電界の強さE 　（70pm75、67am74、61.51） $$E＝\frac { g }{ 4π・r^{ 2 }・ε }　［N/C＝V/m］$$ ・電気力線　（70am75.pm75、67am74) 　電荷から放射性に発生し、電界を形成する仮想的な線　数はQ /ε本出る　正電荷から垂直に出て負電荷で終わる　（単独の場合は無...

・抵抗・コンデンサ・コイル / 直流回路 / 並列回路

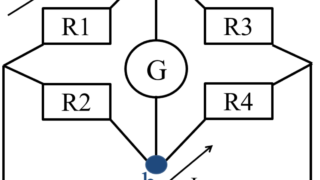
抵抗・コンデンサ・コイル / 直流回路 / 並列回路

抵抗・コンデンサ・コイル抵抗R 　（72am75、65.56、64.52、63.53、62.55）　単位：Ω(オーム)＝1/S(ジーメンス) 　電流の流れにくさを表す　電流の流れやすさはコンダクタンスという　抵抗R＝ρ×長さl［m］÷断面積S［m2］　　　　ρ：抵抗率（比抵抗）［Ω・m］ *倍率器(73pm77) コンデンサ・静電誘導　　導体外部からの電界により電荷が導体表面に移動する現象・静電容量（71am75、70pm75、69pm75、68pm76、67am74、61.51）　単位：F（ファラド）　二つの導体（コンデンサ）に電圧Vを印加すると+q、-qの電界が誘起される　静電容量C　＝　q / V［F＝A・s/V＝C/V］　蓄積されるエネルギーW　＝　CV2×1/2 ・平行平板コンデンサの静電容量C［F］　（72am77）　C［F］＝ε×S［m2］÷d［m］　ε：誘電率・交流回路では電圧Vの位相は、電流Iに対して90°遅れる　Vc　＝　1/wc　×　I0　×　sin(wt-π/2) コイル...

・交流電力 / 変圧器 / 時定数 / 鉄心 / 真空管

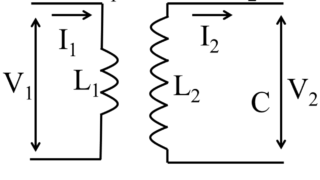
交流電力 / 変圧器 / 時定数 / 鉄心 / 真空管

交流電力（73pm75、68pm76、67pm77、66.53、65.53、61.55）　一周期にわたる瞬時電力pの平均値を交流電力という・交流電力P　　P＝VIcosθ［W］　VI：皮相電力　cosθ：力率・無効電力P　　P＝VIsinθ［W］・実効値＝最大値（瞬時値）/√2 ・平均値＝2/π×最大値（瞬時値）・消費電力P（電力の瞬時値の時間平均）　P＝V×I×cosθ 　V：実効値　I：実効値　　cosθ：位相差変圧器の原理　（72am5、70am77、69am77）　a＝　V2/V1 　　＝　N2/N1 　　　＝　I1/I2 　一次等価抵抗R1＝r1+r2/a2 　二次等価抵抗R2＝r2+a2×r2 　定格容量P＝V2×I2＝V1×I1 変圧器の損失（73pm76、72pm76）・損失W 　W＝鉄損+銅損　　鉄損＝銅損：変圧器の最大効率 1, 無負荷損(鉄損)：鉄心に生じる損失　1-1, ヒステリシス損　1-2,うず電流損 2,負荷損(銅損)：負荷電流によ...

・半導体 / 様々なダイオード

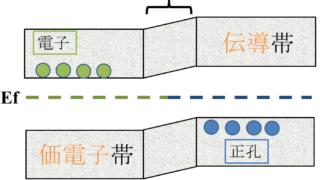
半導体 / 様々なダイオード

固体素子(半導体) 固体の帯理論・真性半導体　（69pm78）　伝導電子の密度n と正孔の密度p が等しい半導体　フェルミ準位はバンドギャップの中央に位置する・n 形半導体　（69pm78、66.56、60.56）　真性半導体に不純物を入れ、自由電子を生じさせ、伝導電子密度n＞正孔密度pとする　キャリア：電子　不純物(ドナー)：Siの場合Sb、P、As 　(いずれも15 族元素) ・p 形半導体　（71pm77、60.56）　真性半導体に不純物を入れ、正孔を生じさせ、正孔密度p＞伝導電子密度nとする　キャリア：正孔　不純物(アクセプタ)：Siの場合B、Al、Ga、In 　(いずれも13 族元素) ・フェルミ準位　（66.56、60.56）　電子の存在確率が1/2のエネルギーのところ　真性半導体：バンドギャップ(価電子帯のすぐ上の禁止帯)の中央　n 形半導体：中央から伝導帯に近づいた位置　p 形半導体：中央から価電子帯に近づいた位置・抵抗率　（69pm78）　絶縁体の抵抗率は1014［Ωm］　シリ...

・増幅器

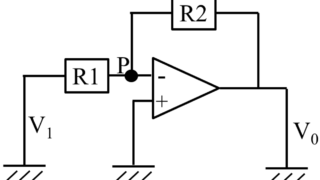
増幅器

増幅器　　電圧増幅度AV＝V2 / V1 　電流増幅度AI＝I2 / I1 　電力増幅度Ap＝V2I2 / V1I1 　　　　　　　　＝P2 / P1 増幅度(利得、ゲイン) （62.54、61.54）　電力増幅度Gp＝10log10P2 / P1［dB］　電圧or電流増幅度Gp＝20log10V2 / V1［dB］　　　　　　　　　　　＝20log10A2 / A1［dB］・オフセット電圧：入力端子を短絡して0Vとした場合に、出力される電圧・デシベルの計算　A dB + B dB = ( A+B ) dB 帰還回路（負帰還回路）　Av ＝ V2 / Vi 　V2 ＝ Av × Vi 　　　= Av ( V1 + βV2) 　帰還後の電圧利得Avf 　Avf＝ V2 / V1 　　　= Av / (1-βAv) ・安定性　Avが変化しても、回路の利得はβによってほぼ決定されるので、極めて安定している演算増幅器（オペレーションアンプ）・反転増幅器　(70pm77、64.57) ...

学生の多くが苦手だと思われる嫌われ科目トップの医用工学
この科目が得意だという学生にはほとんど出会ったことがありません
実際、無理ゲーな問題の出題割合も高めだったりして鬼門なのは確かです
しかし、丸暗記で乗り切れる問題もあるので、全てをあきらめるのではなく、ある程度山を絞って、０点をしっかりと回避しましょう　

「オフラインでも対策ノートが見たい」
「広告が邪魔」
という声にお応えしたく、
電子書籍版（Kindle）の対策ノートを
用意しました！

医用工学
対策ノート
Kindle版

対策ノートの使い方

・オレンジ色の場所を覚える
　オレンジの文字は暗記用赤シートで消えます

・★マーク：特に重要な箇所

・出題年数の見方
　例：（71pm72、67pm13.pm75、66.26）
　71pm72　→　第71回の午後72問
　67pm13.pm75　→　第67回の午後13と75問
　66.26　→　第66回のその教科がある方の26問
（放射化学から医用画像情報学までは午前
　基礎医学大要から安全管理学までは午後）

カテゴリ別に調べたい場合

・PC
　：左カラムの「カテゴリ」
　　または
　　トップページに戻って各教科の「このカテゴリをもっと読む」
　
・スマホ
　：下タブ右側の「カテゴリ」
　　または
　　下タブ左側のホームボタンから各教科の「このカテゴリをもっと読む」

調べたい単語がある場合

・PC
：左カラムの「サイト内を検索」に単語を入力

・スマホ
：下タブ中央の「サイト内を検索」に単語を入力