抵抗、コンデンサ、コイル
(73pm77,72am75.77pm75,70am76,66.54)
問1
1種類のキャリアのみを有する半導体の導電率が102S・m-1、移動速度が0.36m2・V-1・s-1であるとき、キャリア濃度[m-3]はいくつか
ただし、キャリアの電荷を1.6×10-19Cとする
=1.7×1021[m-3]
問題だけだと何を言っているのかわからない学生が多く、難問になりそうだが、実はそうでもない、という問題
今回の問題のように、各数字と答えの単位が書いてあり、他に定数を覚えている必要がない場合、出てきている数字の単位(今回であれば3つ)を組み合わせて、答えの単位に合わせるだけで良いので公式等を知らなくても簡単に解けてしまう
今回の場合はSがオームの逆数なのを知っていれば
導電率:S・m-1→Ω-1・m-1→A・V-1・m-1
移動速度:m2・V-1・s-1
電荷:C→A・s
なので、導電率を移動速度と電荷で割ればよいとわかる
問2
平行板コンデンサにおいて、電極間距離を1/2にし、比誘電率を3倍にした場合、静電容量[F]は元の静電容量[F]に比べて何倍になるか
より
=3÷(1/2)=6倍
コンデンサに関してはこの他にも蓄積されるエネルギーなどの式があるので、覚えておく必要がある
問3
図の回路で、コンデンサCを4.8Vに充電した後、スイッチSを閉じた
時間が無限に経過する間に抵抗Rを流れる電子数[個]はいくつか
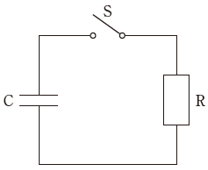
C = 電荷q ÷ 電圧V
より
100×10-6 = q ÷4.8V
Q = 4.8×10-4
電子数[個]=4.8×10-4÷1.6×10-19
=3×1015
回路図にスイッチや抵抗があるので、一見難しそうに見えるかもしれないが、時間が無限に経過するので、非常に単純な問題
これが時間が指定されていたりすると別の式や時定数の概念を把握していないといけないので難しくなってしまうが、それはそれで解けなくてはいけない問題でもあるので注意
また、この問題では電子素量の定数が与えられていないが、計算に必要なため、電子素量を暗記しておく必要があるので、こちらも注意が必要
問4
巻き数が100回のコイル内部の磁束が0.01秒間に0.055Wbから0.040Wbになったときの誘導起電力[V]はいくつか
より、1秒当たりの変化は-1.5Wbなので
V=-100×-1.5=150
1秒当たりに直すことと、マイナスをつけ忘れないことさえできれば簡単
コイルに関してはこの他にも、自己インダクタンスや蓄積されるエネルギーなどの式もあるので覚えておこう
直流回路
(74am76,73pm76,69am75,69pm77,66.52)

問1
図のような抵抗の直並列回路に100Vの直流電圧を加えたときに流れる電流I[A]はいくつか
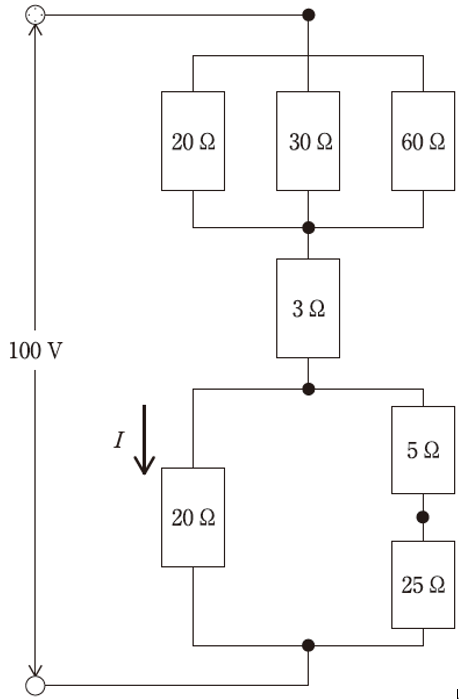
R0=(R1)+3+(R2)
1/R1=1/20+1/30+1/60
R1=10Ω
1/R2=1/20+1/(5+25)
R2=12Ω
R0=25Ω
回路全体に流れる電流I0
I0=100V÷R0
=4A
電流Iのところの電圧V=4A×12Ω=48V
電流I=48/20=2.4A
解法に関してはもっと早いものもあるかもしれないが、ドリルとしては一通り求めてしまったほうが良いかと
注意する点としては、抵抗の並列接続で、3つ以上の場合はR=R1・R2/(R1+R2)の公式は使えないのでR=1/R1+1/R2+1/R3+…+1/Rnのほうで覚えておこう
問2
コンデンサ回路を図に示す
以下に示すものを求めよ
「合成容量」「各コンデンサにかかる電圧」「蓄えられる電荷」「Eの電圧」
ただし、C1の電荷は12μCとする
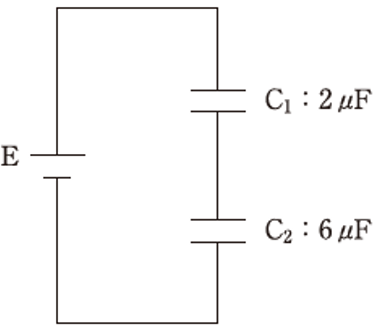
各電圧はV=Q÷Cより
V1=12/2=6
V2=12/6=2
よってE=V1+V2=8V
合成容量C=C1C2/(C1+C2)より、
C=1.5μF
FとCを間違えないように注意が必要
計算自体は簡単なので、法則さえ覚えてしまえば楽だが、抵抗とコンデンサが混在する問題も出題されているのでそちらも解けるようにしておくと万全か
交流回路
(74am75,73pm75,72am76.78,70pm76,68am76,67pm77,66.53)
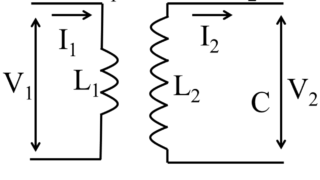
問1
実効値が10Aで位相が正弦波電圧100sin(ωt)[V]よりπ/6ラジアン遅れている正弦波電流の瞬時値を式で示せ
瞬時値=10√2 sin(ωt-π/6)
下記のことを知っているかを試している問題
グラフで出題されても読み取れるようになれるように
・実効値=最大値(瞬時値)/√2
・平均値=2/π×最大値(瞬時値)
・消費電力P(電力の瞬時値の時間平均)
P=V×I×cosθ
V:実効値 I:実効値
cosθ:位相差
問2
下記の図より、消費電力[W]はいくつか
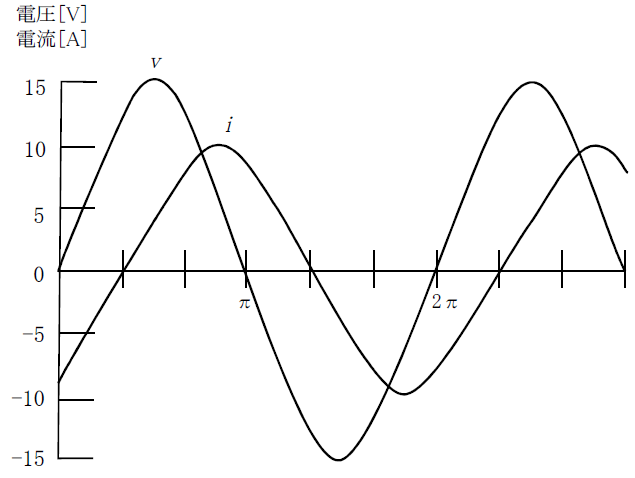
電流の最大値10[A]→実効値10/√2[A]
位相差はπ/3なので消費電力Pは
P=(15/√2)×(10/√2)×cos(π/3)
=37.5W
最大値と実効値の関係を覚えておけば大丈夫
また、cosの計算が出てくるので一通り復習しておいたほうが安心できる
問3
LC回路でC=1nFのとき、50kHzの電磁波を共振させるコイルの自己インダクタンス[H]はいくつか
より
50k=1/{2π√(L×1n)}
よって、
L≒0.01
今回はコイルが穴埋めになったが、周波数やコンデンサが穴埋めになっても解けるように
また、共振の条件に関しても頻出なのでこちらも覚えておく必要がある
変圧器
(72am5,70am77,69am77)

問1
容量30kVA、巻数比N1/N2=30の変圧器で、定格負荷における2次電流[A]はいくつになるか
ただし、N1は1次巻線数、N2は2次巻線数、1次電圧は6kVとして、損失は無視する
定格容量P=V2×I2=V1×I1
より、
1/30 = I1/I2
30k = 6k×I1
I1 = 5A
I2 = 30×5 =150A
1次側からみてどうなるか、2次側からみてどうなるかという問題が電圧電流ともに出うるのですらすらと変換できると大体どの問題も対応できるようになる
二極真空管
(74am77)

問1
二極真空管の空間電荷制限領域で、陽極電圧25V、陽極電流100mAのとき、陽極電圧を9Vとすると陽極電流[mA]はいくつになるか
管電流Ip∝V3/2/d2
より
d2=5/4
なので、V=9Vのときは
Ip=93/2/(5/4)=21.6mA
計算問題に関しては空間電荷制限領域と温度制限領域で式が変わってくるので注意が必要
増幅器
(74pm75)
問1
2つの増幅器を直列に接続した回路を下記に示す

増幅器1の電圧増幅度は10とする
入力電圧Viの値として0.2mVの信号を加えたとき、出力電圧V0の値は0.2であった
このとき、増幅器2の電圧利得[dB]はどれか
増幅器2の電圧利得は
Gp=20log10V2 / V1[dB]より
Gp=20log10(0.2 /2m)=40
増幅度と利得[dB]で計算を混乱してしまわないように注意が必要
(70pm77,64.57) (72pm77,66.57) (73pm78,66.57) (65.57) (61.56) (71pm78)
問2
図に示したオペレーションアンプ回路において、出力電圧V0[V]はいくつか
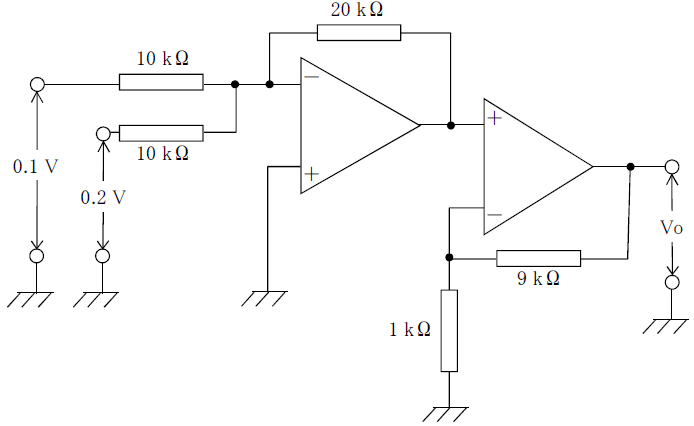
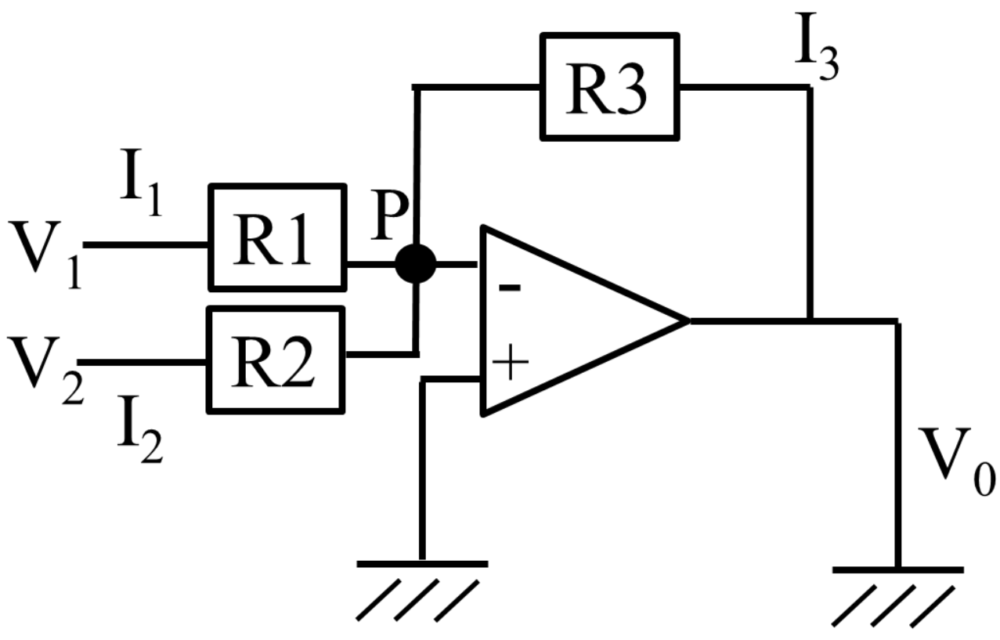
V3 = R3 ( I1 + I2 )
= R3 ( V1 / R1+V2 / R2 )
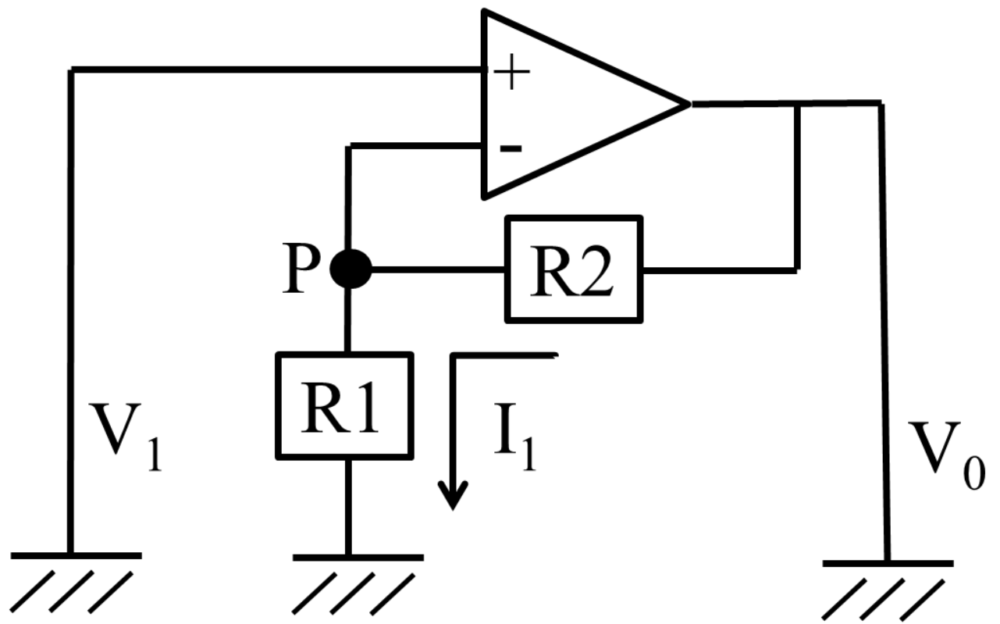
V0=(1+R2 / R1)×V1
より
一段目の回路の出力をV1とすると
V1=-20×(0.1/10 + 0.2/10)
=-0.6
V0=(1+9/1)×-0.6=-6V
計算は各演算器で得られる電圧の式を暗記していないと解けない
ちなみにここ10数年のデータから、出題された演算器を種類別にみてみると、反転増幅器と非反転増幅器と反転加算器が多く、逆に反転減算器、反転積分器、反転微分器は一度ずつしか出題されていない
反転積分に関しては計算問題ではなく、回路図を指定する問題で、形さえ覚えていれば良い問題になっており、反転減算、反転微分に関しても、形を見てどういう演算をするのかさえ把握していれば解けるような形式の問題となっているので、まずは形と名前の一致を重視したい
その後、余裕があれば反転増幅器、非反転増幅器、反転加算器の計算式を覚えるとすべての問題に対応できるようになる





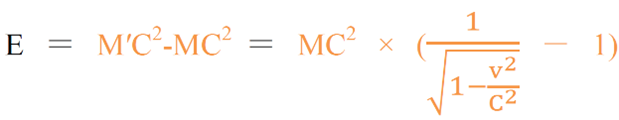
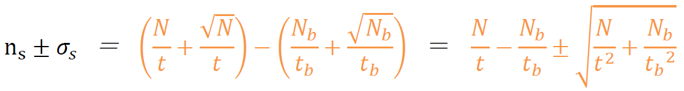

コメント