放射線基本量の単位
(77pm68、76am74pm79、75am81、74am81、73am78.80、72am81、71am79、70am78.pm79、69am78.pm79、68am78、67am78.pm44、66.60.65、65.58.59.64、64.58.59、63.59.60.65、61.41、62.58.60、61.58.59、60.58.59)
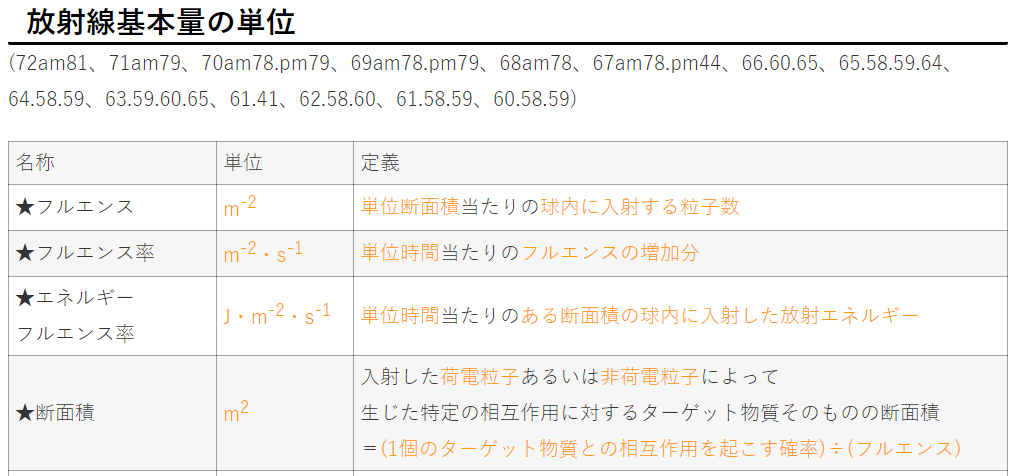
| 名称 | 単位 | 定義 |
| ★フルエンス | m-2 | 単位断面積当たりの球内に入射する粒子数 |
| ★フルエンス率 | m-2・s-1 | 単位時間当たりのフルエンスの増加分 |
| ★エネルギー フルエンス率 |
J・m-2・s-1 | 単位時間当たりのある断面積の球内に入射した放射エネルギー |
| ★断面積 | m2 | 入射した荷電粒子あるいは非荷電粒子によって 生じた特定の相互作用に対するターゲット物質そのものの断面積 =(1個のターゲット物質との相互作用を起こす確率)÷(フルエンス) |
| 線減弱係数 | m-1 | |
| ★質量減弱係数 | m2・kg-1 | 非荷電粒子がある密度の物質中のある距離を通過する間、 作用を起こす割合 |
| ★質量エネルギー 転移係数 |
m2・kg-1 | 非荷電粒子が、ある密度の物質中のある距離を通過する間、 相互作用により荷電粒子(二次電子)の運動エネルギーに付与される 入射粒子の放射エネルギーの割合 |
| ★質量エネルギー 吸収係数 |
m2・kg-1 | =質量エネルギー転移係数×(1-g) g:物質中で制動放射により失われる二次荷電粒子のエネルギーの割合 |
| ★質量阻止能 | J・m2・kg-1 | 荷電粒子がある密度の物質中のある距離を通過する間に失うエネルギー |
| 線エネルギー付与 (LET) |
J・m-1 (keV/μm) |
単位長さあたりに、荷電粒子が電子との衝突により失ったエネルギー ただし、⊿を超える運動エネルギーを有するすべての二次電子の 運動エネルギーの合計は差し引かれている |
| ★放射線化学収率 | mol・J-1 | 単位エネルギー当たりで、 どれくらいその系の物質が変化したかの物質実体の平均量 |
| ★W値 | J | ある気体の一定体積中に吸収された全エネルギーを、 その体積中で生じたイオン対数で除した値 |
| ★カーマ | J・kg-1 =Gy |
ある物質の単位質量あたりに非荷電粒子によって生成された すべての荷電粒子の初期運動エネルギーの総和 =エネルギーフルエンス×質量エネルギー転移係数 |
| ★衝突カーマ | J・kg-1 | =カーマ×(1-g) =エネルギーフルエンス×質量エネルギー吸収係数 |
| ★照射線量 | C・kg-1 | 空気の単位質量当たりに、 光子によって生成した一方の電荷量の絶対値 二次電子の制動放射線を含まない値である |
| ★吸収線量 | J・kg-1 =Gy |
ある物質の単位質量あたりに、 電離放射線により付加された平均エネルギー |
| ★シーマ(セマ) | J・kg-1 | ある物質の単位質量あたりの、 電子衝突で、二次電子を除く荷電粒子のエネルギー損失 |
| 放射能 | s-1 | 単位時間あたりに、放射性核種が壊変する数 |
| 壊変定数 | s-1 | 単位時間当たりに、放射性核種が壊変する確率 |
| ★空気カーマ率定数 | m2・J・kg-1 | 放射能AからLmの距離における空気カーマ率K K=空気カーマ率定数×A/L2 |
照射線量X
(70am81、66.59)
X[C/kg]= Q/mair
= ψ×(μen/ρ)×q÷Wair
mair:空洞空気の質量[kg]
Q:電気量[C]
ψ:エネルギーフルエンス
μen/ρ:質量エネルギー吸収係数
q:素電荷=1.6×10-19[C]
Wair:空気のW値=34eV
光子の吸収線量D
(68pm79)
D[J/kg=Gy]=E×φ×(μen/ρ)
E:光子のエネルギー
φ:フルエンス
荷電粒子の吸収線量D
(66.58)
D=φ×Scol/ρ
Scol/ρ:質量衝突阻止能
β線(電子線)のエネルギー
(70am82、69pm83、66.67、65.67)
最大飛程Rmax = Emax/(Sm×ρ)[cm]
Emax:最大エネルギー
Sm:物質の質量阻止能
ρ:物質の密度
・Feather法
:吸収曲線を利用して電子線の最大エネルギーを求める方法
検出効率
・固有効率
検出器の効率 =「計数された数」÷「入射した数」
「γ線のエネルギー」「検出器の長さ」などに依存
・絶対効率
ある一本のγ線を検出器が計測する確率(幾何学的効率)
絶対効率 =「固有効率」×「立体角」
「γ線のエネルギー」「検出器の長さ」「検出器の半径」「検出器線源間距離」に依存する
・端窓型の幾何効率
(69pm82、67am82、64.66、62.63、60.66)
G = Ω/4π
$$G=\frac { Ω }{ 4π } =\frac { 1 }{ 2 } ×(1-\frac { d }{ \sqrt { d^{ 2 }+r^{ 2 } } } )$$
$$ *r<<dの場合 G=\frac { 1 }{ 4 } ×{ (\frac { r }{ d } ) }^{ 2 }$$
Ω:立体角(4πで幾何学的効率が1となる)
d:試料と検出窓の距離
r:検出半径
・放射能A
A= n ÷ (η×G×f) (64.66)
n:計数率
η:固有効率
f:その他係数
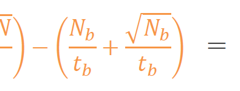








コメント
ψはエネルギーフルエンス、φはフルエンスではないでしょうか。
ご指摘のとおりであります
一部のフォントではファイとプサイのギリシャ文字の区別が付きにくかったため、わざと表記を変えていました
正確な表記の方が良いかと思うので、訂正致しました