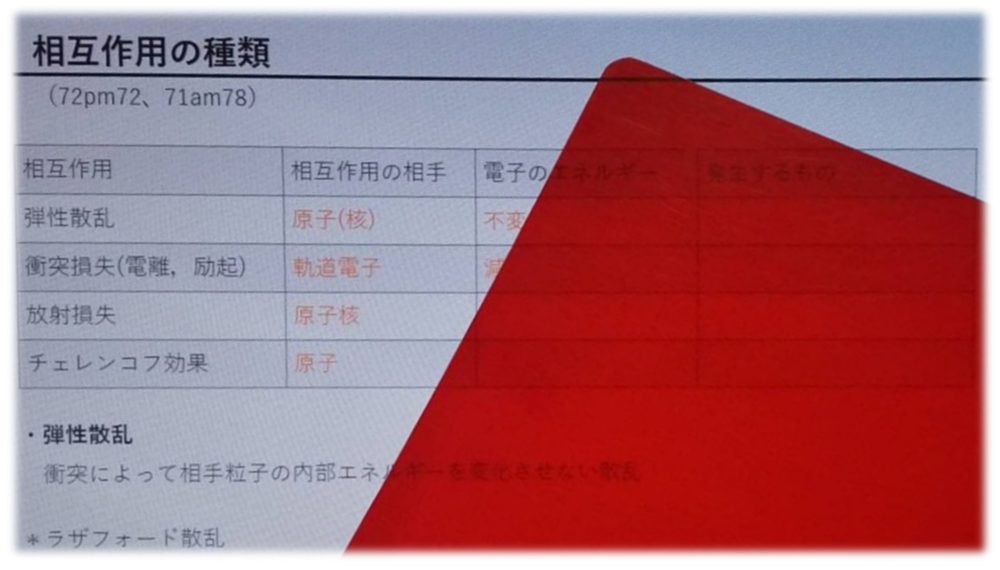
相互作用の種類
(72pm72、71am78)
| 相互作用 | 相互作用の相手 | 電子のエネルギー | 発生するもの |
| 弾性散乱 | 原子(核) | 不変 | なし |
| 衝突損失(電離,励起) | 軌道電子 | 減少 | 特性X線,オージェ電子 |
| 放射損失 | 原子核 | 減少 | 制動X線 |
| チェレンコフ効果 | 原子 | 減少 | 青色光 |
・弾性散乱
衝突によって相手粒子の内部エネルギーを変化させない散乱
*ラザフォード散乱
:ごくまれな確率で原子核と衝突しておこす大角度の散乱
・非弾性散乱
衝突によって相手粒子を励起状態にする場合の散乱
・制動放射 (63.45)
荷電粒子が原子核の電場により制動を受け、そのエネルギーを光子として放出する現象
・電子対消滅 (67am72)
陽電子と電子が対消滅し、その全静止エネルギー(1.022MeV)を180度対向に放出される2つの光子のエネルギー(0.511MeV)として放出する現象
・チェレンコフ放射 (68pm73、63.47、60.48)
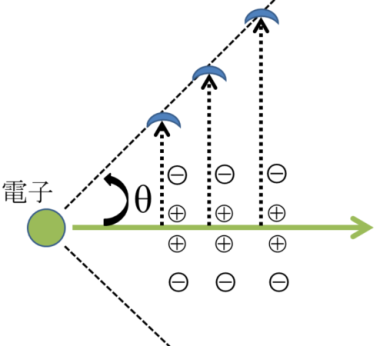
荷電粒子が透明な誘電物質中(屈折率n)を通過するとき、物質中での光の速度(c/n)を超えた速度(v)で移動した場合に、分極によって位相が重なり、可視光(青色)が放出される現象
屈折率nの大きい物質で発生する
発生時間が非常に短く、シンチレーションの発生よりも短い
*臨界エネルギー:n(V/C)≧1
電子の場合:水中で0.26MeV以上で発生
*チェレンコフ光と荷電粒子のなす角θ
cosθ= c/n ÷ v
・核破砕現象(フラグメンテーション)
(66.48)
重荷電粒子では核破砕現象によってブラッグピーク以降にも5~20%ほど線量付与がある
陽電子
(67am72、60.47)
阻止能や飛程など基本的な挙動は電子と同じ
停止時に電子と結合
→ ポジトロニウムの形成
→ 消滅γ線(511keV)を2本以上放出する
・電子対消滅 (67am72)
陽電子と電子が対消滅し,その全静止エネルギー(1.022MeV)を180度対向に放出される2つの光子のエネルギー(0.511MeV)として放出する現象
*電子がない(真空中など)と安定する
阻止能
(75pm71、67am72、68am82)
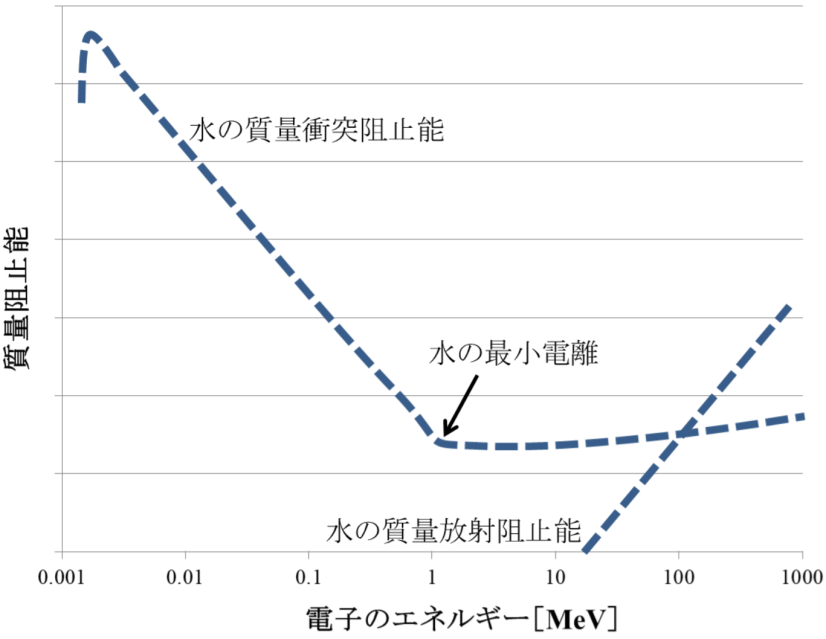
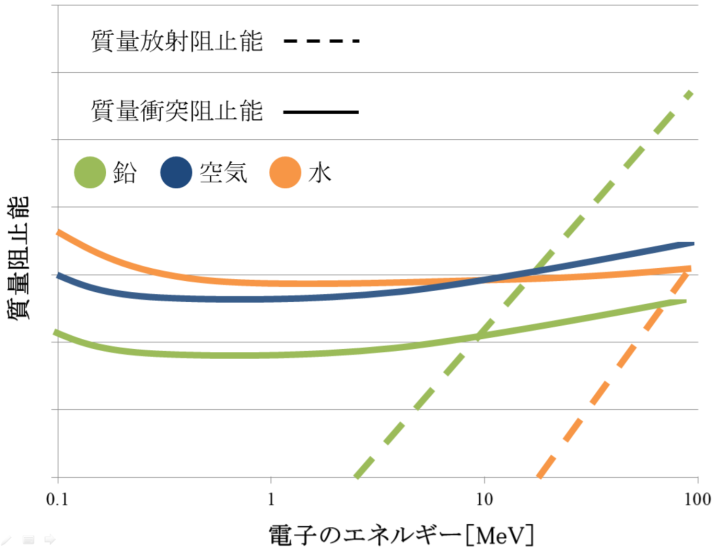
・阻止能
:単位量当たりのエネルギー損失
・全線阻止能S
S=Scol+Srad
・線阻止能S
:単位長さ当たりのエネルギー損失[MeV/mm]
・質量阻止能S/ρ
:線阻止能を密度ρで割った値
・電子の水/空気質量阻止能比
:深部ほど大きくなる
電子の衝突阻止能
(71am73、62.48、60.49)
・線衝突阻止能Scol
$$Scol∝\frac { N×Z }{ mv^{ 2 } } =\frac { ρ×Z }{ mv^{ 2 }×A } $$
→ 密度に比例する
・質量衝突阻止能Scol /ρ
$$ Scol/ρ\quad ∝\quad \frac { 1 }{ mv^{ 2 } } ×\frac { Z }{ A } $$
*N:単位体積あたりの原子数(71am72、66.42)
N = (ρ×NA)/A
Z/Aの値は物質によって変化しない(≒0.5)ため、S/ρは物質の種類に依らない
ρ:密度
NA:アボガドロ数
Z:原子番号
A:物質の質量
m:電子の質量
v:電子の速度
*Bethe Blochらによって量子論的に求められた
*10MeV以上の場合は密度効果を考慮する必要がある
(71am73)
*電子の衝突損失
電子のエネルギーEe<<電子の静止エネルギー
:Scol → 大きくなる
電子のエネルギーEe>>2×電子の静止エネルギー
:Scol → 大きくなる
電子のエネルギーEe=2×電子の静止エネルギー
:Scol → 最小付近
(電子のエネルギーEe<100eV
:Scol → エネルギーの低下とともに小さくなる)
重荷電粒子の衝突阻止能
(76am72、75am72、72am73、71pm70、70pm73、68pm73、67pm79、66.48、65.48、63.49、62.48、60.49)
・衝突阻止能Scol
Scol ∝ z2/v2
∝ (z2/E)×m
電子の放射阻止能
(69pm71、64.47、60.49)
・線放射阻止能Srad
Srad ∝ N×Z2×(E+mc2)
= Z/A×ρ×Z×(E+mc2)
・質量放射阻止能Srad/ρ
Srad/ρ ∝ Z/A×Z×(E+mc2)
Z/Aの値は物質によって変化しないため、原子番号に依存する
重荷電粒子の放射阻止能
(67pm79、66.48、60.49)
荷電粒子の質量が大きいため無視できる
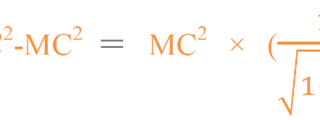
電子の放射阻止能と衝突阻止能の比
(73am72、70am73、68am73、66.46、61.49)
Srad/Scol = (E+0.511)× Z ÷ 820
E:電子のエネルギー[MeV]
Z:物質の原子番号
・臨界エネルギー
:同物質においてSrad=Scolとなるエネルギー
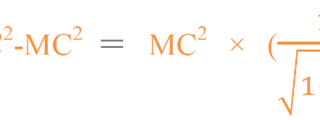
後方散乱
(75am79)
多重散乱により起こり、薄い試料等での測定に影響を与える
線源支持体が厚い程、原子番号が高い程、影響が大きい
(正比例ではなく飽和係数がある)
飛程
電子の飛程
(74am72、65.47)
・電子線の飛程 R
R ≒ 0.5E‐0.3[cm](E=5~50MeV)
≒ 0.54E-0.13[g・cm-2](0.8MeV<E<3MeV)
→ 質量が小さいため、散乱を受ける
重荷電粒子の飛程
(75am40、74pm73、72am44、69am73、67pm74.79、63.49)
・重荷電粒子の飛程 R
$$ R\quad ∝\quad \frac { 1 }{ M } ×(\frac { E }{ Z } )^{ 2 }\quad ∝\quad \frac { M }{ Z^{ 2 } } ×{ v }^{ 4 }$$
R≒0.3E3/2
E:荷電粒子のエネルギー
v:荷電粒子の速度
z:荷電粒子の原子番号
m:荷電粒子の原子番号
・最大飛程 > 外挿(実用)飛程 > 平均飛程
・質量が大きいため、水中では基本的に進行方向は変わらず、直進する
・ブラッグピーク
:停止付近(飛程)で阻止能(比電離)が大きくなる
・陽子の飛程
:水中で200MeVで25.96cm
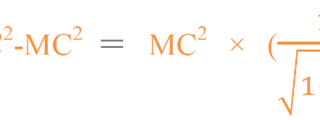
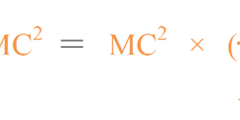





コメント