その他検出器
化学線量計
(69am79)
・鉄線量計(フリッケ線量計)
(69pm80、67pm80、63.64)
酸化反応 [ Fe2+ → Fe3+ ] を利用する
空気か酸素を飽和させて使用する
G値:15.5
・セリウム線量計
還元反応 [ Ce4+ → Ce3+ ] を利用する
G値:2.4
*G値
:溶液が100eVのエネルギーを吸収したときの原子の変化数
イオン濃度と線量率には影響されず、LETには依存する
熱量計(カロリーメータ)
(69pm82、68am80、62.59)
放射線による温度上昇によって放射能を測定する
・水の比熱:4.2 (J/g・K)
1℃=1K-273.15
飛程検出器
・霧箱 (68am80、63.61)
過飽和状態のアルコール気体中に荷電粒子が走行し、その飛程に沿って電離が起こり、このイオンを核として、霧が生じ、その飛程を光で照らして観察を行う
・原子核乾板 (63.61、61.64)
ガラスに厚さ500μm程度にハロゲン化銀を湿布したもので、現像すると荷電粒子の飛程に沿って黒化像として記録される
・固体飛程検出器(CR-39)
絶縁性固体で飛程に沿って生じたエッチピットを測定する
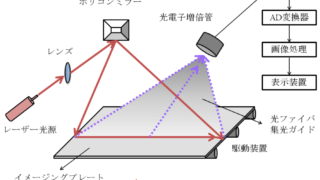
・イメージングプレート
(72am7、66.63、60.63)
測定対象:光子/α/β
光刺激ルミネッセンスを利用している
(温度が高いほど)フェーディングが大きい
・FPD
・ラジオクロミックフィルム(ガフクロミックフィルム)
(75am82,73am81.82,68pm80,65.63)
人体軟部組織に近いフィルムで照射量に応じて着色される
繰返し読取は可能
読み取り光の波長によって線量濃度特性が変化する
感度とエネルギー応答性がよい
読み取り方向依存性がある
温度依存、時間依存がある
・MOSFET
(66.64)
放射線によって生じた電子正孔対による電流-ゲート電圧カーブのシフトが吸収線量に比例する
繰返し読取は可能
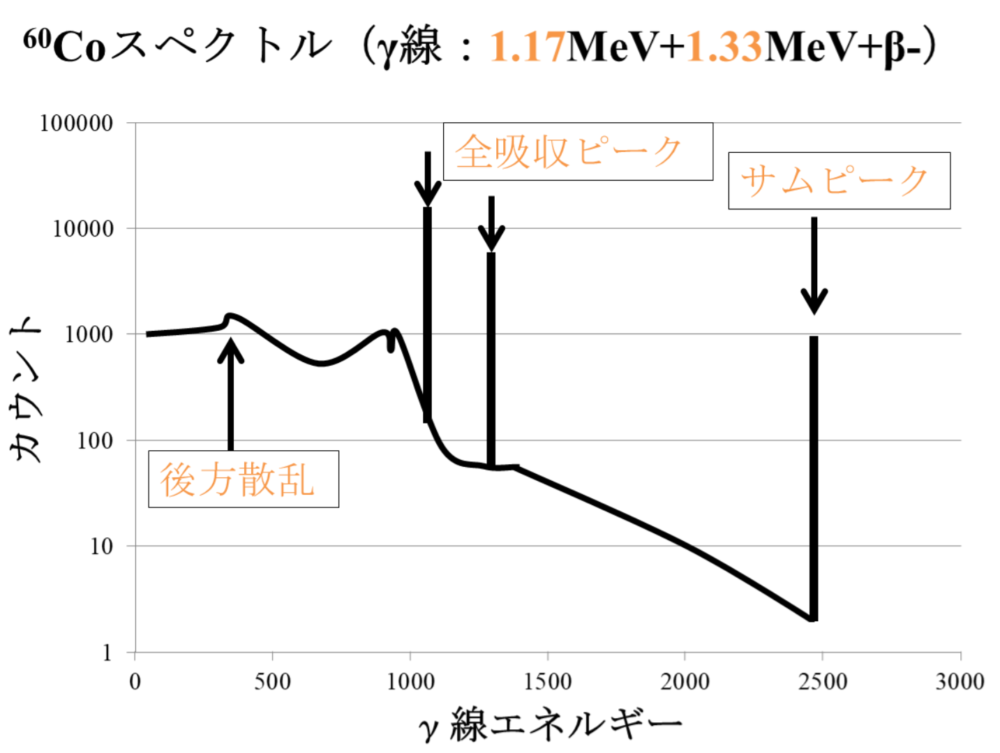
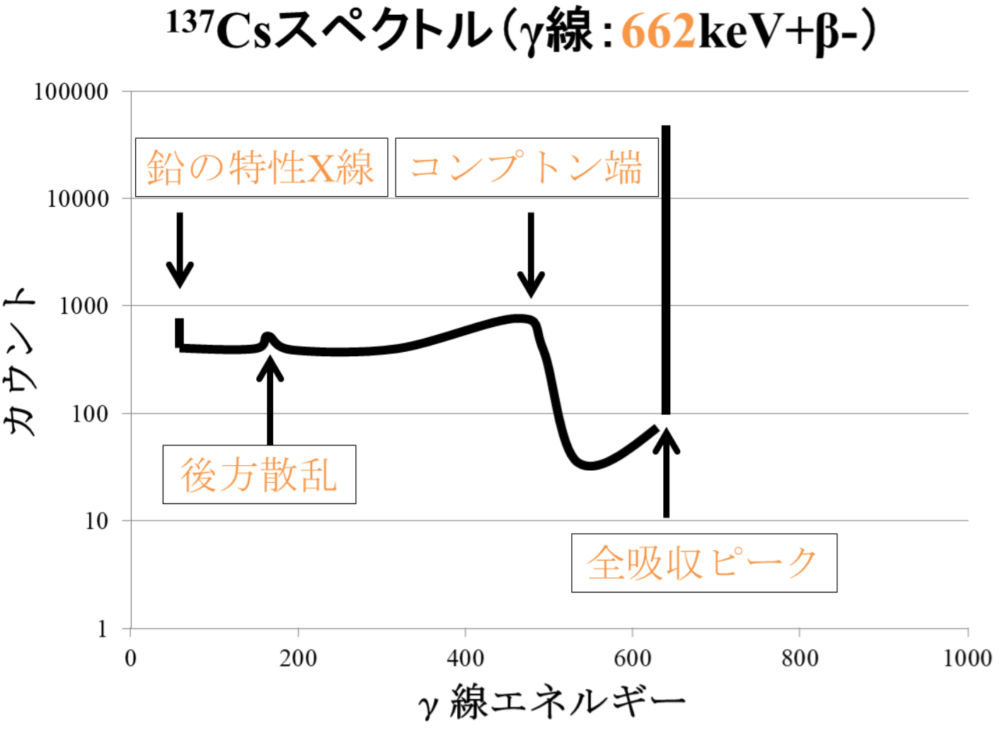
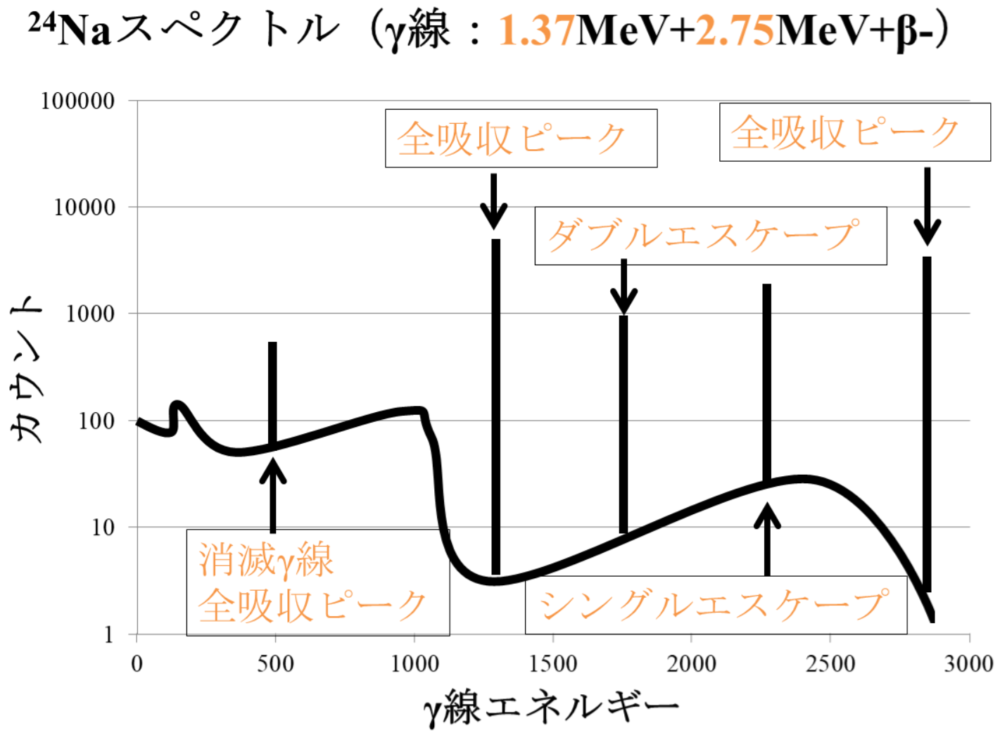
Ge半導体検出器によるスペクトルの測定
(71pm81、69am82、69pm80、69pm83(Co-60)、68pm83(Na-24)、64.67、63.58、61.67(Co-60))
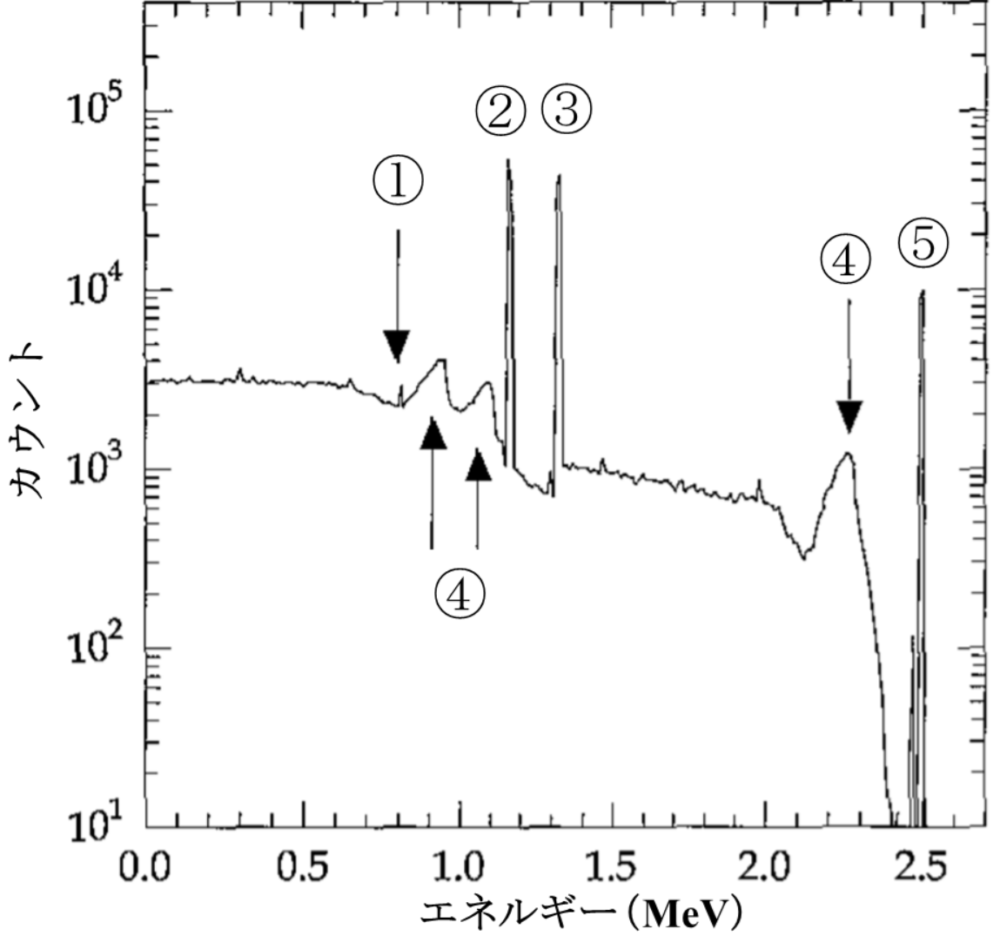
①エスケープピーク
②全吸収ピーク
③全吸収ピーク
④コンプトン端
⑤サムピーク
計数値の統計
・統計的変動
二項分布
→ ポアソン分布
→ 正規分布
(矢印に従い簡略化される)
・計数の標準偏差(σ)
(73pm80、72am79、70am80)
標準偏差σ=√N
N:生の計数(カウント)
N0±σ=68%
N0±2σ=95%
N0±3σ=99.7%
・変動係数CV
(75am78)
変動係数CV=標準偏差σ÷平均値μ
・計数率とその標準偏差σn
(75am80、72pm81、67pm81)
n±σn = N/t ± √N/t
計数率n = N÷t
計数率の標準偏差σn= √N÷t
t:測定時間
・相対誤差
相対誤差 = √N÷N
=1/√N
・誤差の伝播
(65.61)
$$(a±σ_{ a })+(b±σ_{ b })=(a+b)±\sqrt { σ_{ a }^{ 2 }+σ_{ b }^{ 2 } } $$$$(a±σ_{ a })-(b±σ_{ b })=(a-b)±\sqrt { σ_{ a }^{ 2 }+σ_{ b }^{ 2 } } $$$$(a±σ_{ a })×(b±σ_{ b })=(a×b)±(a×b)\sqrt { (σ_{ a }/a)^{ 2 }+(σ_{ b }/b)^{ 2 } } $$$$(a±σ_{ a })÷(b±σ_{ b })=\frac { a }{ b } ±\frac { a }{ b } \sqrt { (σ_{ a }/a)^{ 2 }+(σ_{ b }/b)^{ 2 } } $$
・正味の計数率ns
(68pm81、66.62、61.63、60.61)
$$n_{ s }±σ_{ s }=(\frac { N }{ t } +\frac { \sqrt { N } }{ t } )-(\frac { N_{ b } }{ t_{ b } } +\frac { \sqrt { N_{ b } } }{ t_{ b } } )=\frac { N }{ t } -\frac { N_{ b } }{ t_{ b } } ±\sqrt { \frac { N }{ t^{ 2 } } +\frac { N_{ b } }{ t_{ b }^{ 2 } } } $$
Nb:バックグラウンドの計数
tb:バックグラウンドの計測時間
・一定時間内(T)での標準偏差が最小となる測定時間
$$\frac { t }{ t_{ b } } =\sqrt { \frac { N }{ n_{ b } } } $$$$T=t+t_{ b }$$
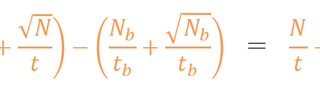
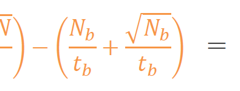






コメント