放射性壊変 / 核分裂

放射性壊変

放射性壊変と放射能

(73pm71、72am71、66.44、65.43、64.44、63.2)
・放射能A　　
　A　＝　-dN/dt　＝　λ×N

・壊変定数λ
　λ　＝　log_e2/T　＝　0.693/T
　T：半減期

・原子数N　
　N　＝　w/W×6.02×10²³
　w：放射性物質の質量
　W：対象物質の原子量

・分岐比λ　
　λ＝λ1+λ2+λ3+……
　λ1，λ2，λ3：部分半減期
　分岐比　→　λ₁：λ₂＝T₂：T₁

・平均寿命τ
　τ＝1/λ＝1.44×T

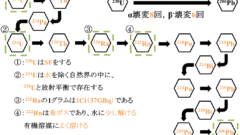
・放射線壊変図
（72am3）

放射化学　計算ドリル　

半減期の計算 (72am71、66.44) 問1 　ある放射性同位元素の放射能を測定したところ1時間後に測定開始時の1/10 となった 　この放射性同位元素の半減期Tはいくつか 　ただし、log102＝0.30とする 答え半減期Tで放射能は1/2になり、1時間後に1/10となるので 1/10 = (1/2)60/T T = 60 log102＝18 解説単位に注意　1時間→60min logの計算はちょいちょい出てくるので基礎的な計算はできるようになっておきたい   問2 　N個の放射性同位元素の放射能をAとしたときに、半減期Tの式を示せ 答えA　＝　λ×N λ　＝　loge2/T T　＝　(N×loge2)/A   解説計算問題ではないが、これらの式の関係を把握しておく必要があるので載せておく 各項に数字を与えられたときに計算できるように   放射化分析の計算 （72pm4） 問 　半減期10分の核種を加速器で製造した 　10分間照射した生成放射能（A1）に対する20分間照射した生成放射能（A2）の比（A2/A1）はいくつか 答え試料を時間t照射して,直後に得られる放射能A A＝f×...

radiological.site

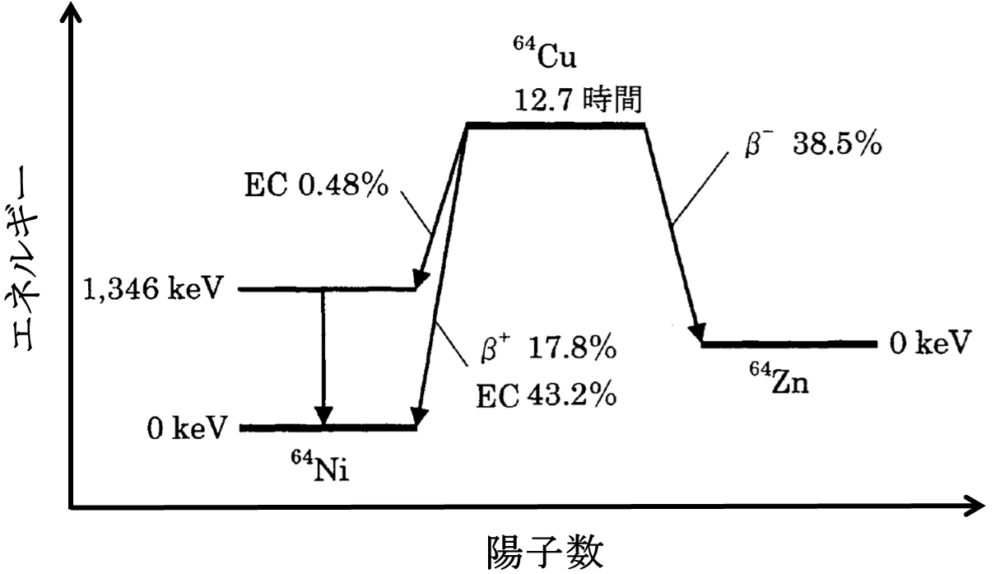
放射平衡

（75pm2,64.2）
・放射平衡
　娘核種の放射能A₂、原子数N₂
$$A_{ 2 }＝\frac { λ_{ 2 } }{ λ_{ 2 }-λ_{ 1 } } ×A_{ 1 }^{ 0 }×({ e }^{ -λ_{ 1 }t }-{ e }^{ -λ_{ 2 }t })+A_{
2 }^{ 0 }×{ e }^{ -λ_{ 2 }t }$$
$$N_{ 2 }＝\frac { λ_{ 1 } }{ λ_{ 2 }-λ_{ 1 } } ×N_{ 1 }^{ 0 }×({ e }^{ -λ_{ 1 }t }-{ e }^{ -λ_{ 2 }t })+N_{ 2 }^{ 0 }×{ e }^{ -λ_{ 2 }t }$$
・過渡平衡　
（70am2、68am2、65.2、65.5）
  成立条件：λ₁＜λ₂、T₁＞T₂
$$A_{ 2 }＝\frac { λ_{ 2 } }{ λ_{ 2 }-λ_{ 1 } } ×A_{ 1 }^{ 0 }$$
$$N_{ 2 }＝\frac { λ_{ 1 } }{ λ_{ 2 }-λ_{ 1 } } ×N_{ 1 }^{ 0 }$$　　
$$Tmax＝\frac { 1 }{ λ_{ 2 }-λ_{ 1 } } ×ln\frac { λ_{ 2 } }{ λ_{ 1 } } $$
　時間経過によって
　A₂＞A₁、T₂→T₁となる

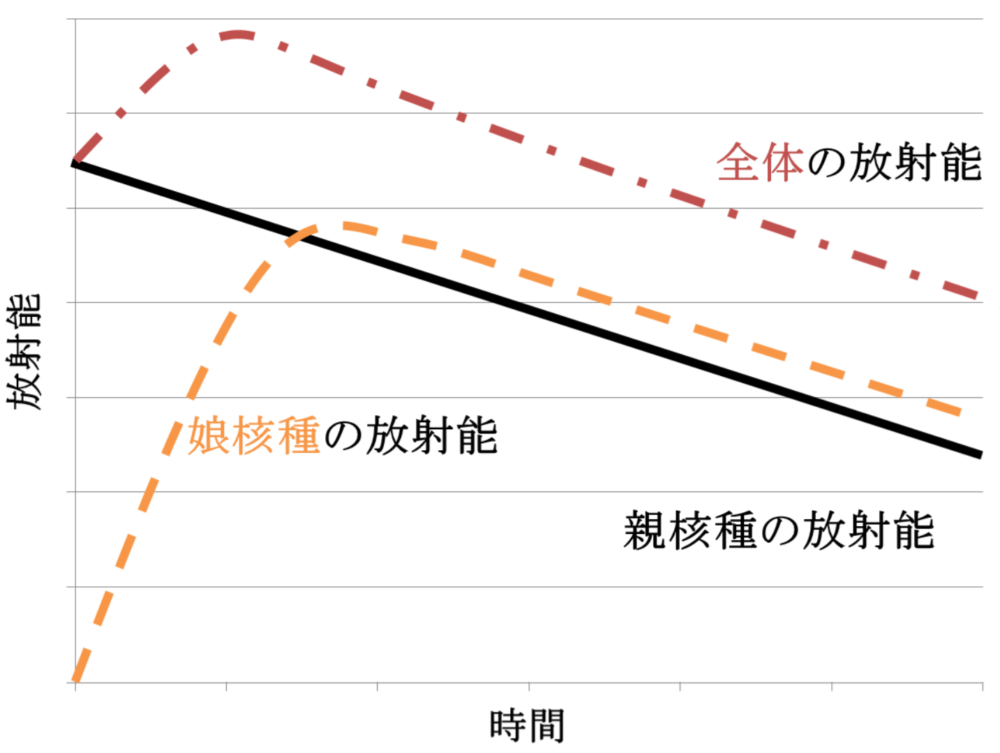
・永続平衡
（73pm2）
　成立条件：λ₁＜＜λ₂、T₁＞＞T₂
　A₂＝A₁⁰
　N₂＝λ₁/λ₂×N₁⁰
　時間経過によって
　A₂＝A₁、T₂→T₁となる

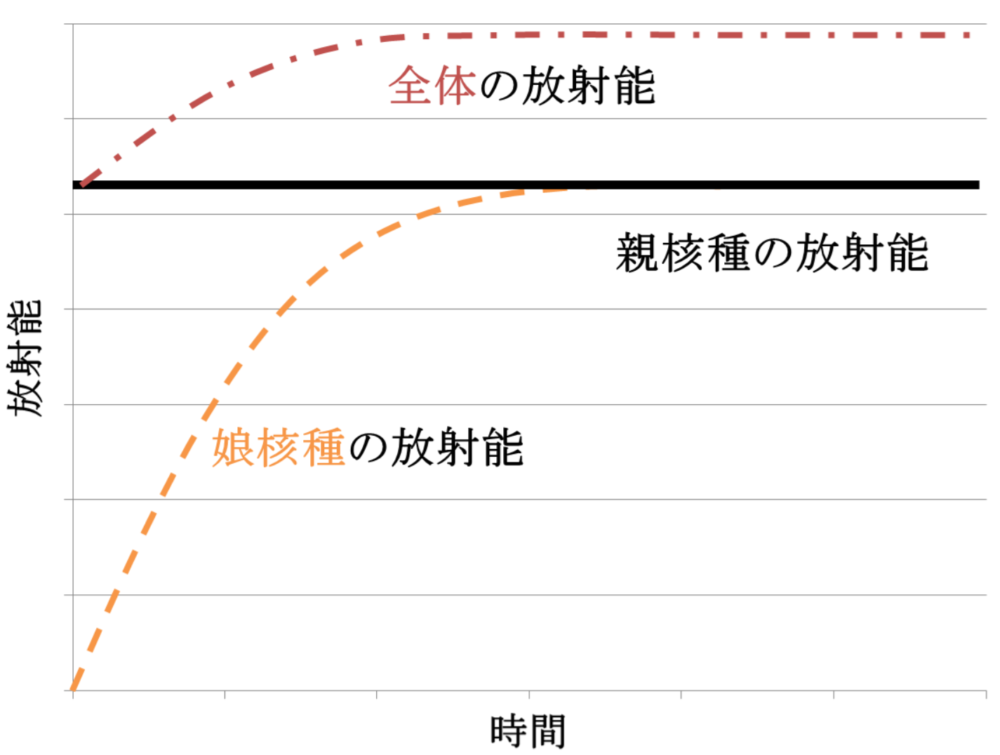
有効半減期Teff

(75pm1、64.2、62.1、60.3)
　Teff＝(Tp×Tb)/(Tb+Tp)
　または、1/Te　＝　1/Tp　+1/Tb
　Tp：物理学的半減期
　Tb：生物学的半減期

核分裂

自発核分裂

　α壊変と同様に、トンネル効果によっておこる

誘導核分裂

　親燃料物質+速中性子
　→　核分裂性物質+速中性子or熱中性子

　核分裂
　→　核分裂生成物+核分裂片

・即発中性子：核分裂直後に放出される中性子
・遅発中性子：核分裂後にやや遅れて放出される中性子

核分裂生成物

　（70pm1、64.3、61.3）
　核分裂の収率の極大は原子量95または138付近