分解時間
(74pm81,69pm81)
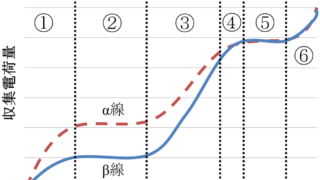
気体の電離を利用する検出器
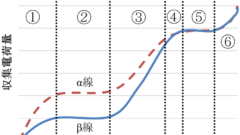
印加電圧と収集電荷の関係 (72am78、66.66、60.62) ①再結合領域 ②電離領域 エネルギー測定可能 ③比例領域 エネルギー測定可能 ④境界領域 ⑤GM領域 エネルギー測定不可 ⑥連...
radiological.site
問1
分解時間100μsのGM計数管で試料を10分間測定して1.2×106カウントを得た
この時の真の計数率［cpm］はいくつか
真の計数率n ＝ m /(1－τ×m)
m：測定した計数率 τ：分解時間［s］
より
m［cps］ ＝ 1.2×106÷（60×10）
＝ 2000
n［cps］ ＝ 2000/（1-（2000×10-4））
＝ 2500
n［cpm］ ＝ 2500×60
＝ 1.5×105
m：測定した計数率 τ：分解時間［s］
より
m［cps］ ＝ 1.2×106÷（60×10）
＝ 2000
n［cps］ ＝ 2000/（1-（2000×10-4））
＝ 2500
n［cpm］ ＝ 2500×60
＝ 1.5×105
GM計数管の分解時間に関する問題
計算式自体は単純なのだが、計数率は大概分あたりのcpmで出題されるのに対して分解時間は秒単位のμsなので単位を合わせて計算するのを忘れないようにしたい
また、カウントで出てきた場合は計数率に変換することも忘れないように
この問題では真の計数率を問うてきているが単位時間当たりで計測されない割合や分解時間を穴埋めで問われても解けるようにしておきたい
計算式自体は単純なのだが、計数率は大概分あたりのcpmで出題されるのに対して分解時間は秒単位のμsなので単位を合わせて計算するのを忘れないようにしたい
また、カウントで出てきた場合は計数率に変換することも忘れないように
この問題では真の計数率を問うてきているが単位時間当たりで計測されない割合や分解時間を穴埋めで問われても解けるようにしておきたい
統計解析
(73pm80,68pm81,67pm81,66.62)
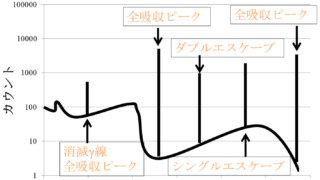
その他検出器 / γ線スペクトル / 計数値の統計
その他検出器 化学線量計 (69am79) ・鉄線量計(フリッケ線量計) (69pm80、67pm80、63.64) 酸化反応 を利用する 空気か酸素を飽和させて使用する G値：15.5 ・セリウム線量計 還...
radiological.site
問1
ある試料を計測したとこと、5分間で800カウント、バックグラウンドが10分間で400カウントだった
正味の計数率［cpm］とその標準偏差はいくつか
正味の計数率ns
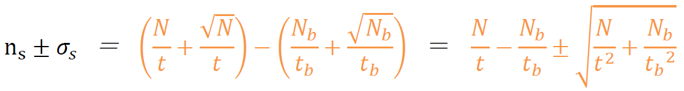
Nb：バックグラウンドの計数
tb：バックグラウンドの計測時間
より
ns±σs＝800/5 – 400/10 ±√（800/25 + 400/100）
＝160 – 40 ± √（32+4）
＝120±6
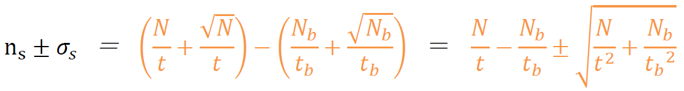
Nb：バックグラウンドの計数
tb：バックグラウンドの計測時間
より
ns±σs＝800/5 – 400/10 ±√（800/25 + 400/100）
＝160 – 40 ± √（32+4）
＝120±6
計数値の統計処理に関する問題
標準偏差や正味の計数率などを聞かれるが、基本的には上記の正味の計数率を誤差込みで覚えてしまえばすべて対応できるはず
標準偏差や正味の計数率などを聞かれるが、基本的には上記の正味の計数率を誤差込みで覚えてしまえばすべて対応できるはず
コメント