画像工学
ナイキスト周波数(Ｎ)
（69pm30、66.91、64.60、60.94）
「サンプリング周波数の1/2」
「画像に含まれている最高周波数」
Ｎ＝1／2ｄ
d：画素間の距離(サンプリング間隔)
・エリアシング誤差
：複製された高周波成分が低周波成分の領域に折り返される現象
マトリックスサイズを小さくして解決する
角度サンプリング数(N)
N＝π×(S／2d)
S：有効視野(㎜)
d：ピクセルサイズ(㎜)
二次元特性
・零周波数は入力画像のCount値の総和
・縦軸はダイナミックレンジに合わせて強度分布に対数表示する
・横軸は周波数軸でナイキスト周波数は0.5である
・原点対象である
・方向依存性である、スペクトル分布は90°方向
空間周波数と画像データの関係
・低空間周波数領域：情報成分(ボケの成分)
・ターゲットデータ：真の情報成分
・高周波成分領域：統計雑音成分(エッジの成分)
デジタルフィルター
（73am34、68pm29、65.61、63.59、62.59、61.58、60.60）
：「画像フィルタによって画素値を変化させる」
前処理フィルタ
・画像復元用
Wiener
：入力画像と出力画像との間の平均二乗誤差を最小にする復元フィルタ
Metz
：MTFの関数によって表現される復元フィルタ
・画像加工用
Butterworth
：高周波成分をカットし、画像の統計雑音を取り除く(低域通過)。
カットオフ周波数が高ければ、より高い周波数をカットする
スムージングフィルタ
：高周波雑音の除去
再構成フィルタ
（75pm33、71am33、61.55）
・フィルタ補正逆投影法
高周波強調を行って再構成時のボケを補正する(ramp)フィルタ
Ramachandranフィルタ
：高周波領域をサイン関数で遮断したもの
→ 「Shepp＆Logan」
：実空間上でスムージング関数を重畳積分したもの
→ 「Chesler」
表示スケール
カラースケールとグレースケール間で表示を変更しても画素値に変化はない
画像再構成法
逐次近似法
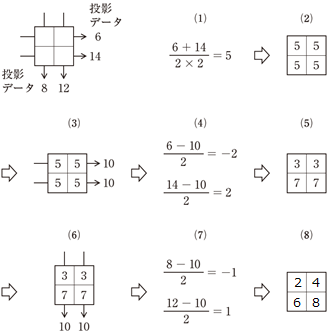(67am92)
・最尤推定―期待値最大化アルゴリズム[ML-EM]
（70pm29、60.57）
長所
① 再構成した画像の画素値が負にならない
② 画素値の総和が保存される
③ 雑音の無いデータでは収束が保証されている
④ 低カウント領域での信号対雑音比が良い
⑤ 高カウント領域からの線状アーチファクトが軽減される
⑥ 測定系で起こる物理現象(減弱、散乱、コリメータ開口特性)を各種補正で織り込むと定量性の向上が期待
短所
① 計算に長時間を要する
② 雑音に対する高速が無いため逐次近似の回数とともに雑音が増加する
③ 収束速度が空間周波数に依存する
・OS-EM法
（74am33、67pm28、64.57）
：投影像をいくつかのサブセットに分割して逐次近似を行う
長所
：画素値の総和が保存されるのはML-EMと同じ
① ML-EM法より高速
② サブセットを増やせばより早くなる
③ 線状アーチファクトが少ない
短所
① 適切な初期値を必要とする
・RAMLA法
：代数的再構成法を基にしたもの
コメント