論理回路
論理回路とドモルガンの法則
(77pm32、75pm46、74am45、72am45、71am46、69pm45、68pm45、67am46、66.90、65.90、64.90)
・NOT:否定 ![]()
・OR:論理和 ![]()
・AND:論理積 ![]()
・XOR:排他的論理和![]()
・NOR:否定論理和 ![]()
・NAND:否定論理積 ![]()
・ドモルガンの法則 (70pm45、61.57、60.57)
論理和の否定は、否定の論理積に等しい
![]()
論理積の否定は、否定の論理和に等しい
![]()
2進法、10進法、16進法
(76am46、75pm47、72pm45、70am45、69am45、68am45、67am45、66.89、65.89、64.89、63.57、61.98)
・16進法 → 10進法
10進法で0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15に対応するのが
16進法で0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
つまり10→A、11→B、12→C、13→D、14→E、15→Fとなる
16進法でABCD
→ 10(A)×163+11(B)×162+12(C)×161+13(D)×160
= 40960+2816+192+13=43981
・2進法→10進法
11111111=27+26+25+24+23+22+21+20
=128+64+32+16+8+4+2+1=255
・2進法→16進法
11111111
→ 1111 1111
=23+22+21+20 23+22+21+20
=15 15=F F
→ FF
・2進法→8進法
11111111
→ 11 111 111
=21+20 22+21+20 22+21+20
=3 7 7
=377
*2進法で負を表すには「符号付2進数」を使い、
最大位が正負(0なら+、1なら-)を表す
・10進法→2進法
(○の部分を下から順に左から右へ並べていく)
170÷2=85+0
85÷2=42+1
42÷2=21+0
21÷2=10+1
10÷2=5+0
5÷2=2+1
2÷2=1+0
1÷2=0+1
→ 10101010
*小数点以下は×2して、一の位を上から同じように並べる
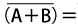
フーリエ変換
・フーリエ変換
$$F(ω)=\int _{ -∞ }^{ ∞ }{ f(t){ e }^{ -iωt }dt }$$
・フーリエ逆変換
$$f(t)=\frac { 1 }{ 2π } \int _{ -∞ }^{ ∞ } F(ω){ e }^{ iωt }dω$$
・フーリエ変換の性質
(77pm31、75am49、73am46、72am47、71pm45、69am48、68am47、62.93)
(1)対称性
a1f1(t) + a2f2(t) ⇀↽ a1F1(ω) + a2F2(ω)
フーリエ変換は,ある波形を異なる振幅や周波数,位相をもつ数多くの正弦波に分解する
フーリエ逆変換は,分解された数多くの正弦波を重ね合わせて元の波形を再生する
(2)線形性
F(t) ⇀↽ 2πf(-ω)
(3)時間軸と周波数軸の推移
f(t – t0) ⇀↽ F(ω) e-iωt0
f(t)eiω0t ⇀↽ F(ω – ω0)
(4) 偶関数、奇関数
偶関数をフーリエ変換した場合、虚数部が消えて実部のみとなる
奇関数をフーリエ変換した場合、偶数部が消えて虚部のみとなる
(5) パーシバルの定理
:関数の平方の積分とそのフーリエ変換の平方の積分とが等しい(ユニタリである)
ある二つの関数の畳み込み積分のフーリエ変換は、それぞれの関数のフーリエ変換の積で表される
(6)パワースペクトル
パワースペクトルは画像をフーリエ変換して得たスペクトルの絶対値の二乗
・パルス信号のフーリエ変換
(73am94、69am94、66pm88)

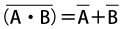









コメント