電荷・電界・電位差(電圧)
電荷(量)Q
単位:C(クーロン)
電荷素量e
e = 1.602×10-19[C]
2個の静電荷に働くクーロン力
(63.51)
クーロン力F
$$F=\frac { 1 }{ 4πε_{ 0 } } ×\frac { g_{ 1 }×g_{ 2 } }{ r^{ 2 } } =9×{ 10 }^{ 9 }×\frac { g_{ 1 }×g_{ 2 } }{ r^{ 2 } }$$
r:距離 g:電荷 ε0:真空の誘電率
電界(1つの電荷が力を及ぼす空間)
電界の強さE
E = 「電気力線の数」÷「表面線[m2]」
・点電荷から距離r[m]での電界の強さE
(70pm75、67am74、61.51)
$$E=\frac { g }{ 4π・r^{ 2 }・ε } [N/C=V/m]$$
・電気力線 (70am75.pm75、67am74)
電荷から放射性に発生し、電界を形成する仮想的な線
数はQ[C] /ε本出る
正電荷から垂直に出て負電荷で終わる
(単独の場合は無限点)
電界の方向を示す(接線方向)
電気力線の密度は電界の強さを示す
交わったり、枝分かれせず、滑らかな線である
・等電位面(線)
電気力線と直交する
電位
(70pm75、67am74、61.51)
単位:V(ボルト)[ J/C=(N・m)/C]
均一な電界Eの中で、電界の方向に距離d離れた位置の電位差V
V=E×d[V]
磁界・磁気力・磁気モーメント
磁極間に働く力(磁気力)F
(77pm65、70am76)
$$F=比例定数k×\frac { m_{ 1 }×m_{ 2 } }{ r^{ 2 } } $$
r:距離
m:磁極の強さ[Wb=V・s](ウェーバ)
磁界(磁極が磁気力を及ぼす空間)
・磁界の強さH
単位:[ J/C=(N・m)/C=A/m] (61.51)
・距離rでの磁気力F[N]
$$F=\frac { m }{ 4π・{ r }^{ 2 }・μ } $$
μ:透磁率
・磁力線
基本的に電気力線と同じ
数はm[Wb] /μ本出る
・磁束密度B = 磁場
(69am75、68pm75、66.51、63.52、60.54)
単位[T(テスラ)=Wb/m2 =μ×H]
磁気モーメント
(66.51、62.52)
磁界Hに磁極mを置いたときに受ける回転力T
T = l×m×H×sinθ[N・m]
l:磁石の長さ[m]
m:磁極の強さ[Wb]
l×m:磁気モーメント
電流I
(65.51、61.52)
・単位:A(アンペア)=C/s
直流電流に垂直な半径r[m]上には磁界Hが発生する
磁界の方向は右ねじを回す方向(右ねじの法則)
・アンペールの法則 (66.51)
磁界H[A/m]=「電流I」÷「磁界の長さm」
=I÷2πr
・ビオ・サバールの法則 (67pm76)
位置rにおける、電流による磁束密度Bを表す式
電流に対して直角方向の磁界の強さが最大となる
電磁力・電流力・ローレンツ力
電磁力
(67pm76)
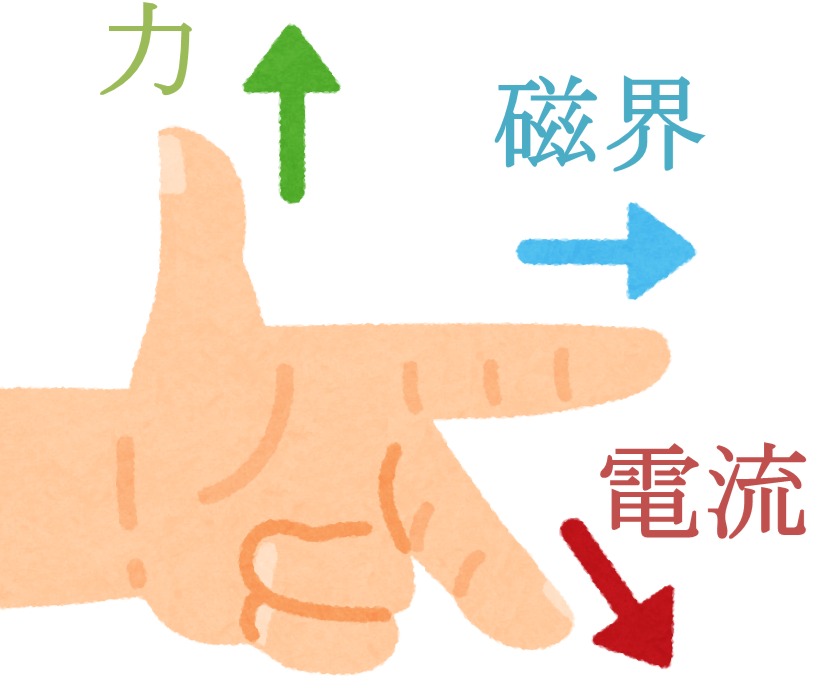
方向:フレミングの左手則
大きさF = μ×H×l×I×sinθ
= B×l×I×sinθ
μ:透磁率
H:磁界[A/m]
I:電流[A]
l:長さ[m]
B:磁束密度
電流力
(67pm76)
ローレンツ力F
F = μ×H×e×v
= B×e×v
v:電荷の速度[m/s]






コメント